How does Kyber Encryption Work
Table of Contents
1. 简介
Kyber 是一种后量子(Post-Quantum Cryptography)公钥加密算法,能够抵抗量子计算机的攻击,本文将介绍它。
2. Baby Kyber
下面我们将介绍 Baby Kyber,它和常规 Kyber 相比,安全参数更小,只保留了最核心的过程,比如省略了对密文的压缩等。这样使得 Baby Kyber 的可读性更好,方便理解。
与其他公钥系统一样,Kyber 也需要一个模数 \(q\) 。也就是说,每次我们用数字进行计算时,我们都会对结果取模。对于 Baby Kyber,我们将此模数指定为 \(q = 17\) 。
对于 Kyber,我们必须处理多项式。由于我们将多项式相乘和相加,我们将对多项式进行模多项式运算,否则他们的次数会变得太大而我们无法处理。我们将使用的多项式模数是 \(f=x^4 + 1\) ,这将保证多项式的次数(最高指数)小于 4。
下面的所有计算都隐含着 1. 对多项式的系数进行模数 \(q=17\) 计算,2. 对多项式本身进行模 \(f=x^4+1\) 多项式运算。
注:如果您不了解多项式模多项式的运算,可以参考 Cryptography and Network Security - Principles and Practice, 8th edition, 5.5 Polynomial Arithmetic
2.1. Key Generation
Kyber 的私钥 \(\mathbf{s}\) 由一些随机多项式组成,且要求它们的系数值很小。关于要求系数值很小的原因可参见节 2.3.1 。
对于 Baby Kyber 来说,假设私钥 \(\mathbf{s}\) 为两个多项式 \[\mathbf{s} = \begin{pmatrix} -x^3 - x^2 + x \\ -x^3 -x \\ \end{pmatrix}\] 它们是随机产生的多项式系数很小的多项式。注: “系数很小”的意思是“和 \(0\) 或者系数模数 \(q=17\) 比较接近”。 上面的私钥 \(\mathbf{s}\) 中多次出来的 \(-1\) 系数做个模 \(17\) 运算后就是 \(16\) ,尽管和 \(0\) 比不是很接近,但它和模数 \(17\) 很接近,所以也符合“系数很小”的要求。
Kyber 的公钥由两部分组成:随机矩阵多项式 \(\mathbf{A}\) 和另一个矩阵 \(\mathbf{t}\) 。 在 Baby Kyber 例子中,将使用 \[\mathbf{A} = \begin{pmatrix} 6x^3 + 16x^2 + 16x + 11 & 9x^3 + 4x^2 + 6x + 3 \\ 5x^3 + 3x^2 + 10x + 1 & 6x^3 + x^2 + 9x + 15 \end{pmatrix}\] 前面提到过 Bady Kyber 中,对多项式的系数进行模数 \(q=17\) 计算,对多项式本身进行模 \(f=x^4+1\) 多项式运算,所以 \(\mathbf{A}\) 的多项式系数都小于 \(17\) ,且多项式次数都小于 \(4\) 。
Kyber 公钥中另一部分 \(\mathbf{t}\) 的计算公式为 \[\mathbf{t} \triangleq \mathbf{A}\mathbf{s} + \mathbf{e}\] 其中 \(\mathbf{e}\) 是错误矩阵,要求是随机产生,且多项式的系数比较小。在 Baby Kyber 例子中,将使用 \[\mathbf{e} = \begin{pmatrix} x^2 \\ x^2 -x \\ \end{pmatrix}\]
从而,我们可以计算出公钥 \(\mathbf{t}\) 为 \[\begin{aligned}\mathbf{t} &\triangleq \mathbf{A}\mathbf{s} + \mathbf{e} \\ & = \begin{pmatrix} 16x^3 + 15x^2 + 7 \\ 10x^3 + 12x^2 + 11x + 6 \end{pmatrix} \end{aligned}\]
2.1.1. 依赖的数学难题(Module-LWE)
前面介绍了 Kyber 私钥 \(\mathbf{s}\) 和公钥 \(\mathbf{A},\mathbf{t}\) 符合关系 \(\mathbf{t} = \mathbf{A}\mathbf{s} + \mathbf{e}\) 。
已知 \(\mathbf{A},\mathbf{t}\) ,很难恢复出 \(\mathbf{s}\) ,这被称为 Module Learning With Errors(Module-LWE)问题,这对于量子计算机也很难,这就是 Kyber 所依赖的数学难题。
2.2. 加密
对于非对称加密系统来说,使用公钥对消息进行加密,使用私钥对消息进行解密。
Kyber 加密时,会使用 2 个一次一用的系数比较小的随机矩阵 \(\mathbf{r},\mathbf{e_1}\) ,和 1 个一次一用的系数比较小的随机多项式 \(e_2\) 。 在 Baby Kyber 例子中,将使用 \[\begin{aligned}\mathbf{r} & = \begin{pmatrix} -x^3 + x^2 \\ x^3 + x^2 - 1 \end{pmatrix} \\ \mathbf{e_1} & = \begin{pmatrix} x^2 + x \\ x^2 \end{pmatrix} \\ e_2 & = -x^3 - x^2 \end{aligned}\]
在加密消息前,我们需要先把消息编码为某个多项式。 我们可以使用消息的二进制表达作为多项式的系数。比如我们想加密数字 \(11\) ,它的二进制表达为 \((1011)_2\) ,所以待加密的数字 \(11\) 可以编码为多项式 \(m_b = 1x^3 + 0 x^2 + 1x^1 + 1 x^0 = x^3 + x + 1\)
在加密前,还需要把 \(m_b\) 的系数放大,这是通过乘以 \(\lceil \frac{q}{2} \rfloor\) 来实现的(为什么在加密前要把 \(m_b\) 放大呢?其原因可参考节 2.3.1)。其中记号 \(\lceil x \rfloor\) 表示最接近实数 \(x\) 的整数,如果实数 \(x\) 恰好位于两个连续整数中间,则上向取整,比如 \(\lceil 1.4 \rfloor = 1, \lceil 1.5 \rfloor = 2\) 。在我们的例子中,有 \(\lceil \frac{q}{2} \rfloor = \lceil \frac{17}{2} \rfloor = \lceil 8.5 \rfloor = 9\) 。
也就是说待加密的数字 \(11\) 最终编码为了 \[m \triangleq \lceil \frac{q}{2} \rfloor \cdot m_b = 9 x^3 + 9x + 9\]
使用公钥 \(\mathbf{A}, \mathbf{t}\) 对消息 \(m\) 进行加密,其密文由两个部分组成 \((\mathbf{u},v)\) ,它的定义为 \[\begin{aligned} \mathbf{u} & \triangleq \mathbf{A}^{\mathsf{T}} \mathbf{r} + \mathbf{e_1} \\ v & \triangleq \mathbf{t}^{\mathsf{T}} \mathbf{r} + e_2 + m \end{aligned}\]
代入各个值,我们可以计算出数字 \(11\) 的密文的两个部分 \((\mathbf{u},v)\) 分别为 \[\begin{aligned} \mathbf{u} &= \begin{pmatrix} 11x^3 + 11 x^2 + 10 x + 3 \\ 4x^3 + 4x^2 + 13x + 11 \end{pmatrix} \\ v &= 8x^3 + 6x^2 + 9x + 16 \end{aligned}\]
2.3. 解密
使用私钥 \(\mathbf{s}\) 可对密文 \((\mathbf{u},v)\) 进行解密,解密步骤如下。
第一步,使用下面公式计算出带有噪声的解密结果(noisy result) \[m_{\text{noisy}} \triangleq v - \mathbf{s}^{\mathsf{T}} \mathbf{u}\] 代入私钥和密文的具体值,可得 \[m_{\text{noisy}} = 8x^3+14^2+8x+6\]
第二步,检查 \(m_n\) 的各个系数,看它是更接近于 \(\lceil \frac{q}{2} \rfloor = 9\) ,还是更接近于 \(0\) (或者 \(q=17\) )。如果更接近于 \(\lceil \frac{q}{2} \rfloor\) ,则把系数改为 \(\lceil \frac{q}{2} \rfloor\) ;如果更接近于 \(0\) (或者 \(q=17\) ),则把系数改为 \(0\) 。下面依次检测一下 \(m_n\) 的各个系数。
- 系数 \(8\) 更接近于 \(9\) ,所以改为 \(9\)
- 系数 \(14\) 更接近于 \(0\) (或者 \(q=17\) ),所以改为 \(0\)
- 系数 \(8\) 更接近于 \(9\) ,所以改为 \(9\)
- 系数 \(6\) 更接近于 \(9\) ,所以改为 \(9\)
所以,得到解密多项式 \(9x^3 + 0 x^2 + 9x + 9\) ,可以发现它就是加密前的多项式。
第三步,把多项式的缩小 \(\lceil \frac{q}{2} \rfloor = 9\) 倍,就得到原始加密数据的二进制表达 \[m_b = \frac{1}{\lceil \frac{q}{2} \rfloor}(9x^3 + 0 x^2 + 9x + 9) = x^3 + 0 x^2 + x + 1\]
所以,我们得到二进制数据 \((1011)_2\) ,换算为十进制就是 \(11\) ,它就是原始加密数据。
2.3.1. 解密的原理
为什么 \(m_{\text{noisy}}\) 是带有噪声的解密结果呢?我们按照 \(m_{\text{noisy}}\) 定义展开一下 \[\begin{aligned} m_{\text{noisy}} & \triangleq v - \mathbf{s}^{\mathsf{T}} \mathbf{u} \\ & = \mathbf{t}^{\mathsf{T}} \mathbf{r} + e_2 + m - \mathbf{s}^{\mathsf{T}} (\mathbf{A}^{\mathsf{T}} \mathbf{r} + \mathbf{e_1}) \\ & = (\mathbf{A}\mathbf{s} + \mathbf{e})^{\mathsf{T}} \mathbf{r} + e_2 + m - \mathbf{s}^{\mathsf{T}} (\mathbf{A}^{\mathsf{T}} \mathbf{r} + \mathbf{e_1}) \\ & = \underbrace{\mathbf{e}^{\mathsf{T}} \mathbf{r} + e_2}_{\text{系数很小}} + m - \underbrace{\mathbf{s}^{\mathsf{T}} \mathbf{e_1}}_{\text{系数很小}} \end{aligned}\]
前面提到过,生成 \(\mathbf{e},\mathbf{r},e_2,\mathbf{s},\mathbf{e_1}\) 时,要求多项式的系数很小;而对于消息 \(m\) 特意把它系数放大了。
所以, \(m_{\text{noisy}}\) 中的大头是 \(m\) ,其它项全面加起来也只是微不足道的噪声。
3. Kyber 总结
Kyber 加解密的总结如图 1 所示(改编自 https://youtu.be/gp7KFOs7y3g?t=3818 中截图)。
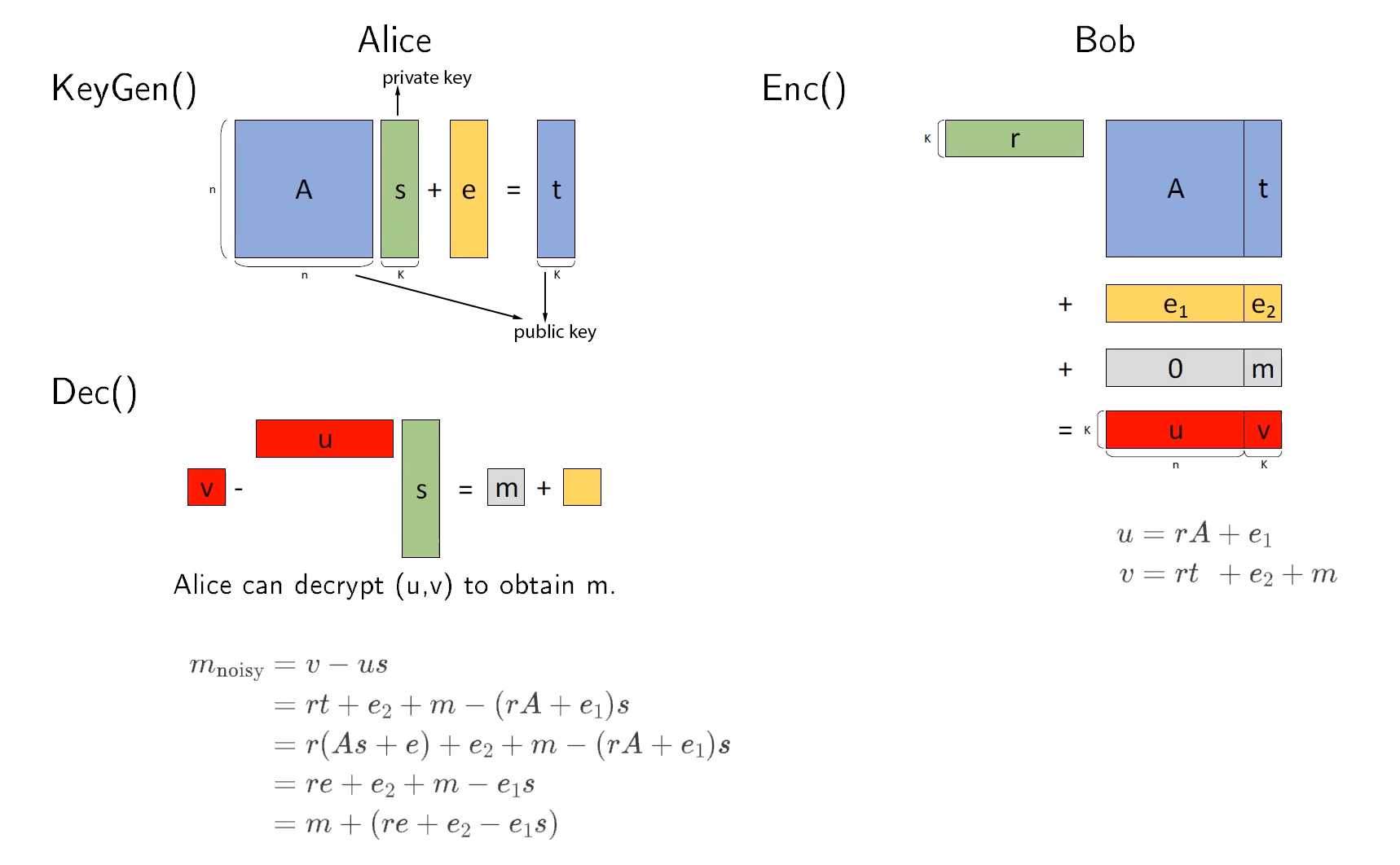
Figure 1: Kyber 总结
需要注意的是,图 1 中采用的定义是 \(u = rA + e_1, v = rt + e_2 + m, m_{\text{noisy}} = v - us\) ,而 Kyber 论文(以及前面的例子)采用的定义是 \(u = A^{\mathsf{T}}r + e_1,v = t^{\mathsf{T}}r + e_2 + m, m_{\text{noisy}} = v - s^{\mathsf{T}}u\) ,为什么会有区别呢?其实它们是完全一样的,只是因为图 1 中 \(r,e_1\) 是“行向量”定义形式,而 Kyber 论文(以及前面的例子)中 \(r,e_1\) 是“列向量”定义形式,行向量和列向量之间有个“矩阵转置操作”的区别,这导致 \(u,v,m_{\text{noisy}}\) 的形式有小的区别。
4. Kyber 和 ElGamal 的相似之处
从形式上看,Kyber 和 ElGamal 有相似之处,它们的密文都由两部分构成,而且每部分的产生过程也比较类似,如表 1 所示。从形式上说,可以认为 Kyber 是一种 noisy ElGamal 算法。
| ElGamal 加密 | Kyber 加密 |
|---|---|
| 密文第 1 部分 \(c_1 = g^r\) | 密文第 1 部分 \(u=A^{\mathsf{T}} r + e_1\) |
| 密文第 2 部分 \(c_2 = m \cdot h^r\) | 密文第 2 部分 \(v=m + t^{\mathsf{T}} r + e_2\) |
| \(r\) 是一次一用随机数 | \(r\) 是一次一用随机数 |
| \(h\) 是公钥 | \(t\) 是公钥 |
5. 参考
- 原论文 CRYSTALS – Kyber: a CCA-secure module-lattice-based KEM
- Kyber - How does it work?(本文 Bady Kyber 的例子来源这个文章,注:本文修正了这个文章中的几处错误)
- Cryptography and Network Security - Principles and Practice, 8th edition, 5.5 Polynomial Arithmetic
- CRYSTALS – Kyber and Dilithium, by Peter Schwabe
6. 附录
6.1. Baby Kyber 示例代码
# polynomials/modules from: https://github.com/GiacomoPope/kyber-py
from polynomials import *
from modules import *
q = 17
n = 4 # x^4 + 1
R = PolynomialRing(q, n)
M = Module(R)
s0 = R([0,1,-1,-1])
s1 = R([0,-1,0,-1])
s = M([s0,s1]).transpose()
A00 = R([11,16,16,6])
A01 = R([3,6,4,9])
A10 = R([1,10,3,5])
A11 = R([15,9,1,6])
A = M([[A00, A01],[A10, A11]])
e0 = R([0,0,1,0])
e1 = R([0,-1,1,0])
e = M([e0,e1]).transpose()
t = A @ s + e
print("s:",s)
print("A:",A)
print("e:",e)
print("t:",t)
r0 = R([0,0,1,-1])
r1 = R([-1,0,1,1])
r = M([r0, r1]).transpose()
print("r:",r)
e1_0 = R([0,1,1,0])
e1_1 = R([0,0,1,0])
e1 = M([e1_0, e1_1]).transpose()
print("e1:",e1)
e2 = M([R([0,0,-1,-1])])
print("e2:",e2)
m = M([R([9,9,0,9])])
# Encryption
u = A.transpose() @ r + e1
v = t.transpose() @ r + e2 + m
print("u:", u)
print("v:", v)
# Decryption
m_noisy = v - s.transpose() @ u
print("m_noisy:", m_noisy) # m_noisy: [6 + 8*x + 14*x^2 + 8*x^3]