Logistic Regression
Table of Contents
1. Logistic 回归简介
假设我们想对一些数据进行二分类处理。我们希望有这么一个函数能接受所有的输入,且输出只有二个值:如 0 或者 1。单位阶跃函数(Heaviside step function)就是一个满足这个条件的函数,但单位阶跃函数不是连续的,在跳跃点从 0 突然跳跃到 1,这有时比较难处理。Sigmoid 函数(又称为 Logistic 函数)是另一个具有类似性质的函数,Sigmoid 函数如下:
\[\sigma(z) = \frac{1}{1+ e^{-z}}\]
其对应的曲线图(和单位阶跃函数很像)如图 1 所示。
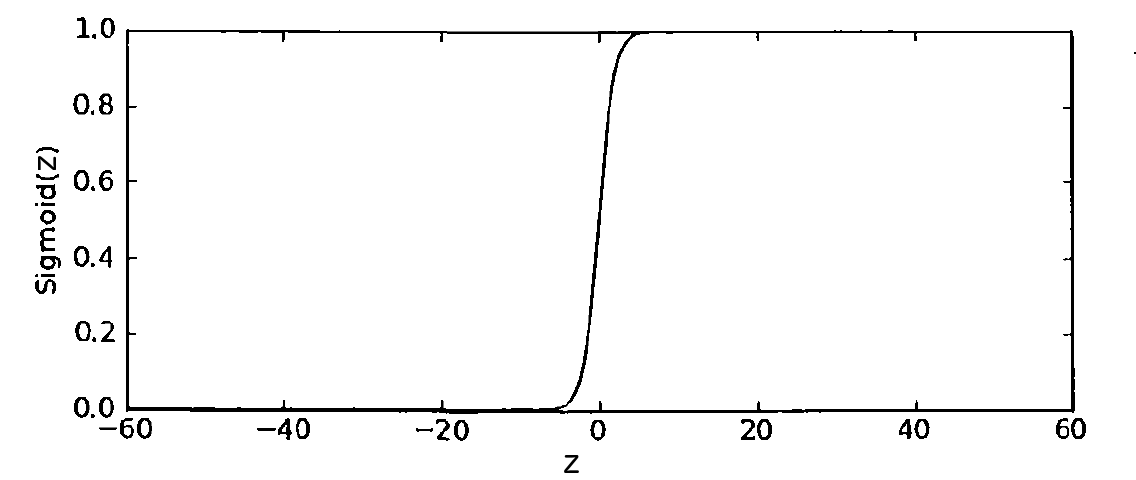
Figure 1: Sigmoid Function
当自变量为 0 时,Sigmoid 函数值为 0.5,随着自变量的增大,对应的 Sigmoid 值将逼近于 1;随着自变量的减小,对应的 Sigmoid 值将逼近于 0。
参考:机器学习实战,第 5 章 Logistic 回归
1.1. Logistic 回归分类器
Logistic 回归分类器的思路为:我们把每个特征上都乘以一个系数,然后把所有结果值相加(还可能加上一个偏置量),将这个总和代入 Sigmoid 函数中,这将得到一个范围在 0 到 1 之间的数值,如果大于 0.5,则把数据归为 1 类;如果小于 0.5,则把数据归入 0 类。
即 Sigmoid 函数的输入由下式得到:
\[z = b + w^{(1)} x^{(1)} + w^{(2)} x^{(2)} + \cdots + w^{(n)} x^{(n)}\]
若把 \(w^{(0)}\) 当作 \(b\) ,把 \(x^{(0)}\) 当作 1。可记 \(\boldsymbol{w} = (b, w^{(1)}, w^{(2)}, \cdots, w^{(n)})^{\mathsf{T}}, \, \boldsymbol{x} = (1, x^{(1)}, x^{(2)}, \cdots, x^{(n)})^{\mathsf{T}}\) ,上式的向量形式为:
\[z = \boldsymbol{w}^{\mathsf{T}} \boldsymbol{x}\]
则 Logistic 回归模型可写为(下式中, \(\boldsymbol{w}\) 和 \(\boldsymbol{x}\) 都是向量):
\[\sigma = \frac{1}{1+ e^{- \boldsymbol{w}^{\mathsf{T}} \boldsymbol{x}}}\]
1.2. Logistic 回归可看作概率估计
Sigmoid 函数的输出值在 0 到 1 之间,所以 Logistic 回归可以看作是概率估计: Logistic 回归的输出看作是 \(y=1\) 的概率。
\[P(Y=1 \mid \boldsymbol{x}) = \frac{1}{1+ e^{- \boldsymbol{w}^{\mathsf{T}} \boldsymbol{x}}}\]
对于给定的输入数据 \(\boldsymbol{x}\) ,计算 \(P(Y=1 \mid \boldsymbol{x})\) ,Logistic 回归的思想就是比较 \(P(Y=1 \mid \boldsymbol{x})\) 和 0.5 的大小关系,大于 0.5 时把数据归到 \(y=1\) 的那类,否则归到 \(y=0\) 的那类。
1.2.1. 用 logit 函数表示 Logistic 回归模型
一个事件的几率(odds)是指该事件发生的概率与该事件不发生的概率的比值。例如,如果事件发生概率为 \(p\) ,则该事件的几率为 \(\frac{p}{1-p}\) 。 事件的对数几率称为 logit 函数 ,即:
\[\operatorname{logit}(p) = \ln \frac{p}{1-p}\]
对于 Logistic 回归模型来说,有:
\[\begin{aligned} \operatorname{logit}(p) & = \ln \frac{p}{1-p} \\
& = \ln \frac{P(Y = 1 \mid \boldsymbol{x})}{ 1 - P(Y = 1 \mid \boldsymbol{x})} \\
& = \ln \frac{\frac{1}{1+ e^{- \boldsymbol{w}^{\mathsf{T}} \boldsymbol{x}}}}{ 1 - \frac{1}{1+ e^{- \boldsymbol{w}^{\mathsf{T}} \boldsymbol{x}}}} \\
& = \boldsymbol{w}^{\mathsf{T}} \boldsymbol{x} \\
\end{aligned}\]
有时,我们用 logit 函数来表示 Logistic 回归模型。
1.3. Logistic 回归模型的参数估计
如何通过训练数据集估计 Logistic 回归分类器的参数向量 \(\boldsymbol{w}\) 呢?
对于给定的训练数据集 \(T = \{ (\boldsymbol{x_1}, y_1), (\boldsymbol{x_2}, y_2), \cdots, (\boldsymbol{x_N}, y_N)\}\) ,其中, \(\boldsymbol{x_i} \in \mathbb{R}^n, y_i \in \{0, 1\}\) ,我们可以利用极大似然估计求得模型参数的估计值。
记 \(\pi(\boldsymbol{x_i}) \overset{\text{def}}{=} \sigma = \dfrac{1}{1+ e^{- \boldsymbol{w}^{\mathsf{T}} \boldsymbol{x_i}}}\) ,则有:
则训练数据集的似然函数为:
\[L(\boldsymbol{w}) = \prod_{i=1}^{N}\pi(\boldsymbol{x_i})^{y_i} (1 - \pi(\boldsymbol{x_i}))^{1 - y_i}\]
其对数似然函数为:
\[\begin{aligned} \ln L(\boldsymbol{w}) & = \sum_{i=1}^{N} \left[ y_i \ln \pi(\boldsymbol{x_i}) + (1 - y_i) \ln (1 - \pi(\boldsymbol{x_i})) \right] \\
& = \sum_{i=1}^{N} \left[ y_i \ln \frac{\pi(\boldsymbol{x_i})}{1 - \pi(\boldsymbol{x_i})} + \ln ( 1 - \pi(\boldsymbol{x_i})) \right] \\
& = \sum_{i=1}^{N} \left[ y_i \ln \frac{\frac{1}{1+ e^{- \boldsymbol{w}^{\mathsf{T}} \boldsymbol{x_i}}}}{ 1- \frac{1}{1+ e^{- \boldsymbol{w}^{\mathsf{T}} \boldsymbol{x_i}}}} + \ln (1 - \frac{1}{1+ e^{- \boldsymbol{w}^{\mathsf{T}} \boldsymbol{x_i}}}) \right] \\
& = \sum_{i=1}^{N} \left[ y_i (\boldsymbol{w}^{\mathsf{T}} \boldsymbol{x_i}) - \ln (1 + e^{\boldsymbol{w}^{\mathsf{T}} \boldsymbol{x_i}}) \right] \end{aligned}\]
对上式求极大值,取极大值时对应的 \(\hat{\boldsymbol{w}}\) 就是 \(\boldsymbol{w}\) 的估计值。
对于最优化问题,我们习惯于解决极小化问题,对上式(对数似然函数)的极大化相当于极小化它的相反数,所以我们可以认为 Logistic 回归的损失函数为对数似然函数的相反数 :
\[\begin{aligned} J(\boldsymbol{w}) & = - \sum_{i=1}^{N} \left[ y_i \ln \pi(\boldsymbol{x_i}) + (1 - y_i) \ln (1 - \pi(\boldsymbol{x_i})) \right] \\
& = - \sum_{i=1}^{N} \left[ y_i (\boldsymbol{w}^{\mathsf{T}} \boldsymbol{x_i}) - \ln (1 + e^{\boldsymbol{w}^{\mathsf{T}} \boldsymbol{x_i}}) \right] \end{aligned}\]
对损失函数最小化,取极小值时对应的参数 \(\hat{\boldsymbol{w}}\) 就是 \(\boldsymbol{w}\) 的估计值。
1.3.1. 用梯度下降法最小化损失函数
可以用梯度下降法求得损失函数最小时对应的参数值。梯度下降法是一种迭代算法,其参数更新公式为:
\[\theta_{new} = \theta_{old} - \mu \nabla f(\theta_{old}) = \theta_{old} - \mu \left. \frac{\partial f}{\partial \theta} \right|_{\theta = \theta_{old}}, \quad \mu > 0\]
我们按下面规则迭代更新 Logistic 回归模型参数 \(\boldsymbol{w}\) 的每一个分量 \(w^{(j)}, \, j=0,1,2,\cdots,n\) 即可:
\[w^{(j)}_{new} = w^{(j)}_{old} - \mu \left. \frac{\partial J}{\partial w^{(j)}} \right|_{w^{(j)} = w^{(j)}_{old}}, \quad \mu > 0\]
上式中的 \(\frac{\partial J}{\partial w^{(j)}}\) 求解过程如下:
\[\small \begin{aligned} \frac{\partial J}{\partial w^{(j)}} & = \frac{\partial}{\partial w^{(j)}} \left( - \sum_{i=1}^{N} \left[ y_i \ln \pi(\boldsymbol{x_i}) + (1 - y_i) \ln (1 - \pi(\boldsymbol{x_i})) \right] \right) \\
& = \frac{\partial}{\partial w^{(j)}} \left( - \sum_{i=1}^{N} \left[ y_i (\boldsymbol{w}^{\mathsf{T}} \boldsymbol{x_i}) - \ln (1 + e^{\boldsymbol{w}^{\mathsf{T}} \boldsymbol{x_i}}) \right] \right) \\
& = - \sum_{i=1}^{N} \frac{\partial}{\partial w^{(j)}} \left( y_i (\boldsymbol{w}^{\mathsf{T}} \boldsymbol{x_i}) - \ln (1 + e^{\boldsymbol{w}^{\mathsf{T}} \boldsymbol{x_i}}) \right) \\
& = - \sum_{i=1}^{N} \frac{\partial}{\partial w^{(j)}} \left( y_i (w^{(0)} x_i^{(0)} + w^{(1)} x_i^{(1)} + \cdots + w^{(j)} x_i^{(j)} + \cdots + w^{(n)} x_i^{(n)}) - \ln(1 + e^{w^{(0)} x_i^{(0)} + w^{(1)} x_i^{(1)} + \cdots + w^{(j)} x_i^{(j)} + \cdots + w^{(n)} x_i^{(n)}}) \right) \\
& = - \sum_{i=1}^{N} \left( y_i x_i^{(j)} - \frac{\partial}{\partial w^{(j)}} \left( \ln(1 + e^{w^{(0)} x_i^{(0)} + w^{(1)} x_i^{(1)} + \cdots + w^{(j)} x_i^{(j)} + \cdots + w^{(n)} x_i^{(n)}}) \right) \right) \\
& = - \sum_{i=1}^{N} \left( y_i x_i^{(j)} - \frac{1}{1 + e^{w^{(0)} x_i^{(0)} + w^{(1)} x_i^{(1)} + \cdots + w^{(j)} x_i^{(j)} + \cdots + w^{(n)} x_i^{(n)}}} e^{w^{(0)} x_i^{(0)} + w^{(1)} x_i^{(1)} + \cdots + w^{(j)} x_i^{(j)} + \cdots + w^{(n)} x_i^{(n)}} x_i^{(j)} \right) \\
& = - \sum_{i=1}^{N} \left( y_i x_i^{(j)} - \frac{e^{\boldsymbol{w}^{\mathsf{T}} \boldsymbol{x_i}}}{1 + e^{\boldsymbol{w}^{\mathsf{T}} \boldsymbol{x_i}}} x_i^{(j)} \right) \\
& = - \sum_{i=1}^{N} \left( y_i x_i^{(j)} - \pi(\boldsymbol{x_i}) x_i^{(j)} \right) \\
& = - \sum_{i=1}^{N} \left( (y_i - \pi(\boldsymbol{x_i}) x_i^{(j)} ) \right) \\
\end{aligned}\]
说明 1:上面的推导过程仅仅用了求导的一些基本知识,如复合函数求导的链式法则(Chain rule),求导公式 \((\ln x)' = \frac{1}{x}, \, (e^x)' = e^x\) 等等。
说明 2:本文中, \(\boldsymbol{x_i}\) 表示训练数据集 \(N\) 条记录中的某一条,而 \(x_i^{(j)}\) 则表示这条记录的第 \(j\) 个特征。这种表示方法和李航著作“统计学习方法”一致;但和 Andrew Ng 的机器学习课程中的表示不一致(Andrew Ng 的课程可参考http://cs229.stanford.edu/notes/cs229-notes1.pdf)。
所以,最后可以得到 Logistic 回归模型参数 \(\boldsymbol{w}\) 的每一个分量 \(w^{(j)}, \, j=0,1,2,\cdots,n\) 的迭代更新公式为:
\[w^{(j)}_{new} = w^{(j)}_{old} + \mu \left. \sum_{i=1}^{N} \left( (y_i - \pi(\boldsymbol{x_i}) x_i^{(j)} ) \right) \right|_{w^{(j)} = w^{(j)}_{old}}, \quad \mu > 0\]
其中, \(\pi(\boldsymbol{x_i}) = \frac{1}{1+ e^{- \boldsymbol{w}^{\mathsf{T}} \boldsymbol{x_i}}}, \; y_i \in \{0, 1\}\)
1.3.2. 用随机梯度下降法加快速度
前面得到的随机梯度下降法参数迭代公式中有 \(\sum_{i=1}^{N}\) ,即用梯度下降法每次更新参数 \(\boldsymbol{w}\) 都要遍历整个训练数据集!如果训练数据非常大时,这将很耗时。
一种改进办法是采用随机梯度下降法(Stochastic Gradient Descent, SGD), 随机梯度下降法每次仅使用一个训练数据来更新参数。 随机梯度下降法的参数迭代公式为:
\[w^{(j)}_{new} = w^{(j)}_{old} + \mu \left. \left(y_i - \pi(\boldsymbol{x_i}) x_i^{(j)} \right) \right|_{w^{(j)} = w^{(j)}_{old}}, \quad \mu > 0\]
其中, \(\pi(\boldsymbol{x_i}) = \frac{1}{1+ e^{- \boldsymbol{w}^{\mathsf{T}} \boldsymbol{x_i}}}, \; y_i \in \{0, 1\}\)
说明 1:随机梯度下降法可以在新训练数据到来时,对 Logistic 回归分类器进行增量式更新,所以 随机梯度下降法是一个“在线”学习算法 ;与“在线”学习相对应,一次处理所有训练数据的方式被称为是“批处理”。
说明 2:应该注意上面的参数迭代公式有一个前提是分类标记 \(y_i \in \{0, 1\}\) ,如果给定的训练数据不是这样(例如为 \(y_i \in \{-1, 1\}\) ),则在使用上面的参数迭代公式时应该把-1 转换为 0。
1.3.2.1. 分类标记 \(y_i \in \{-1, 1\}\) 时的损失函数
前面推导出来的公式,要求 \(y_i \in \{0, 1\}\) ,如果给定训练数据中 \(y_i \in \{-1, 1\}\) ,除了做个简单-1 到 0 的转换外;其实,我们也可以直接采用 \(y_i \in \{-1, 1\}\) ,在这个情况下,其损失函数推导如下。
记 \(\pi(\boldsymbol{x_i}) = \sigma = \dfrac{1}{1+ e^{- \boldsymbol{w}^{\mathsf{T}} \boldsymbol{x_i}}}\) ,有:
从而,似然函数为:
\[\begin{aligned} L(\boldsymbol{w}) & = \prod_{i=1}^{N} P(Y_i = y_i \mid \boldsymbol{x_i}) \\
& = \prod_{i=1}^{N} \pi(y_i \boldsymbol{x_i}) \\
\end{aligned}\]
对数似然函数为:
\[\begin{aligned} \ln L(\boldsymbol{w}) & = \sum_{i=1}^{N} \pi(y_i \boldsymbol{x_i}) \\
& = \sum_{i=1}^{N} \dfrac{1}{1 + e^{- y_i \boldsymbol{w}^{\mathsf{T}} \boldsymbol{x_i}}} \\
\end{aligned}\]
对应的损失函数即为:
\[\begin{aligned} J(\boldsymbol{w}) & = - \sum_{i=1}^{N} \dfrac{1}{1 + e^{- y_i \boldsymbol{w}^{\mathsf{T}} \boldsymbol{x_i}}} \\
& = \sum_{i=1}^{N} \ln (1 + e^{- y_i \boldsymbol{w}^{\mathsf{T}} \boldsymbol{x_i}})\\
\end{aligned}\]
上式中, \(y_i \in \{-1, 1\}\) 。类似地,用梯度下降法可以最小化上面的损失函数,求得参数迭代公式。
参考:
Machine Learning - A Probabilistic Perspective, 8.3.1 MLE
http://beader.me/2014/05/03/logistic-regression/
1.3.3. 选择合适的学习率
梯度下降公式中的学习率(又称步长) \(\mu\) 比较难决定,太小,则更新太慢;太大,则容易矫枉过正。如图 2 (图中用 \(\eta\) 表示学习率)所示。
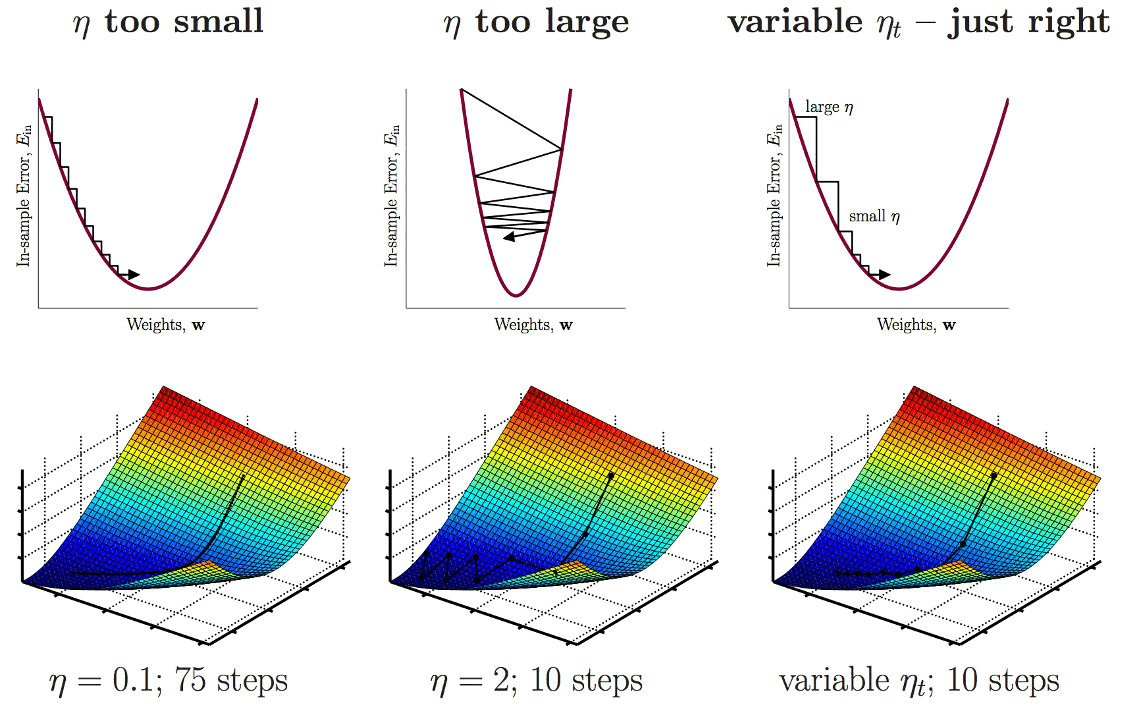
Figure 2: The 'Goldilocks' Step Size
如何选择合适的步长?这个问题没有标准答案,基本上需要通过测试确定。 简单的做法是选择随迭代次数增加而逐渐减小的 \(C/t, C/t^2\) 等。
参考:
http://www.cs.rpi.edu/~magdon/courses/LFD-Slides/SlidesLect09.pdf
https://www.quora.com/What-is-the-best-way-to-choose-the-step-size-in-stochastic-gradient-descent
1.3.4. 为什么不选择平方损失函数
如果使用平方损失函数,则每个数据产生的损失(误差)为:
其中, \(\pi(\boldsymbol{x_i}) = \frac{1}{1+ e^{- \boldsymbol{w}^{\mathsf{T}} \boldsymbol{x_i}}}, \; y_i \in \{0, 1\}\)
使用平方误差和 \(\sum err\) 作为损失也是可以的,但它是关于参数 \(\boldsymbol{w}\) 的非凸函数(non-convex function),这里不证明它。
而对于非凸函数的优化是非常困难的(注:梯度下降法要求被优化函数是凸函数)。非凸函数由于存在很多个局部最小点,比较难去做最优化(求全局最小点)。所以 Logistic 回归不使用平方损失函数。
参考:
http://beader.me/2014/05/03/logistic-regression/
http://www.holehouse.org/mlclass/06_Logistic_Regression.html
1.3.5. 用牛顿法和拟牛顿法最小化损失函数
前面已经介绍过梯度下降法和随机梯度下降法最小化损失函数。牛顿法(Newton method)和拟牛顿法(Quasi-Newton method)也是求解无约束最优化问题的常用方法,可以用来最小化 Logistic 回归模型的损失函数。这里不详细介绍。
牛顿法和拟牛顿法的优点在其收敛速度一般比梯度下降法更快,而且无需手动选择学习率(即步长)。 不过牛顿法和拟牛顿法的计算相对比梯度下降法复杂。
2. Logistic 回归实例
A researcher is interested in how variables, such as GRE (Graduate Record Exam scores), GPA (grade point average) and prestige of the undergraduate institution, effect admission into graduate school. The response variable, admit/don't admit, is a binary variable.
通过“GRE”,“GPA”,“本科学校的等级”三个指标,建立模型来预测“研究生是否录取”。部分的训练数据如下:
## admit gre gpa rank ## 1 0 380 3.61 3 ## 2 1 660 3.67 3 ## 3 1 800 4.00 1 ## 4 1 640 3.19 4 ## 5 0 520 2.93 4 ## 6 1 760 3.00 2
3. 防止“过拟合”
什么是过拟合(overfitting)? 当模型开始拟合训练数据中的噪声时,就称之为过拟合。
图 3 是用多项式拟合曲线的例子,其最右边的子图就是“过拟合”。
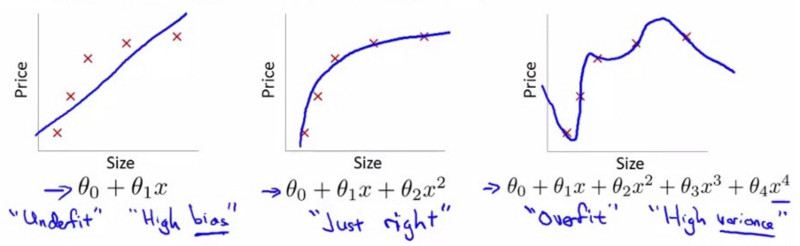
Figure 3: “欠拟合”和“过拟合”
过拟合的模型尽管其训练误差很小,但模型对于它没有见过的数据没有泛化能力,即模型泛化能力太差。
交叉验证和正则化(又称规则化)可以防止过拟合,下文将介绍它们。
3.1. 用交叉验证防止“过拟合”
交叉验证的思想是:模型在拟合过程中不使用全部的历史数据,而是保留一部分数据,用来模拟未来的数据,对模型进行检验。
3.2. 用正则化防止“过拟合”
过拟合一般使模型变得过于复杂。
什么是模型的复杂度呢?如果要给多项式拟合的模型定义复杂度,则可以认为多项式的次数越高模型越复杂,如 5 次多项式模型比 2 次多项式模型要复杂得多。
对于 Logistic 回归,我们可以用特征的权重来表示模型的复杂度。
这样,为了避免过拟合(模型太复杂),我们可以把所有权重之和(为了避免正负抵消,取权重的绝对值)放入到损失函数中。
如,重定义损失函数为:
\[J(\boldsymbol{w}) = - \sum_{i=1}^{N} \left[ y_i \ln \pi(\boldsymbol{x_i}) + (1 - y_i) \ln (1 - \pi(\boldsymbol{x_i})) \right] + \lambda \sum_{j=1}^{n} \left| w^{(j)} \right|\]
上式称为 L1 正则化(L1 regularization) 。式中, \(\lambda\) 用于调节正则化因子所占的比重。
还有其它正则化手段,如定义正则化因子为权重平方和,这称为 L2 正则化(L2 regularization) 。
\[\begin{aligned} J(\boldsymbol{w}) & = - \sum_{i=1}^{N} \left[ y_i \ln \pi(\boldsymbol{x_i}) + (1 - y_i) \ln (1 - \pi(\boldsymbol{x_i})) \right] + \lambda \sum_{j=1}^{n} {w^{(j)}}^2 \\
& = - \sum_{i=1}^{N} \left[ y_i \ln \pi(\boldsymbol{x_i}) + (1 - y_i) \ln (1 - \pi(\boldsymbol{x_i})) \right] + \lambda \boldsymbol{w}^{\mathsf{T}} \boldsymbol{w} \\
& = - \sum_{i=1}^{N} \left[ y_i \ln \pi(\boldsymbol{x_i}) + (1 - y_i) \ln (1 - \pi(\boldsymbol{x_i})) \right] + \lambda \Vert \boldsymbol{w} \Vert^2 \\
\end{aligned}\]
3.2.1. L1 VS L2 Regularization
实际应用时,我们数据的维度可能很高, L1 正则化的一个重要优点是能产生稀疏解(即有很多权重为零),这可以实现“特征选择”。
为了便于可视化,我们考虑两维的情况,如图 4 所示。在 \((w^{(1)}, w^{(2)})\) 平面上画出目标函数的等高线(在图中带有颜色的圈圈上任取 \((w^{(1)}, w^{(2)})\) 后,用它们计算的目标函数值是相等的,离这些圈圈的中心越近,目标函数值越小,在圈圈中心处的目标函数值最小),而约束条件则成为平面上半径为 C 的一个 norm ball 。等高线与 norm ball 首次相交的地方就是最优解。图 4 中的 l1-ball 和 l2-ball 包含的区域是解空间。我们只能在这个解空间中,寻找使得目标函数最小的 \(w^{(1)}\) 和 \(w^{(2)}\) 值。
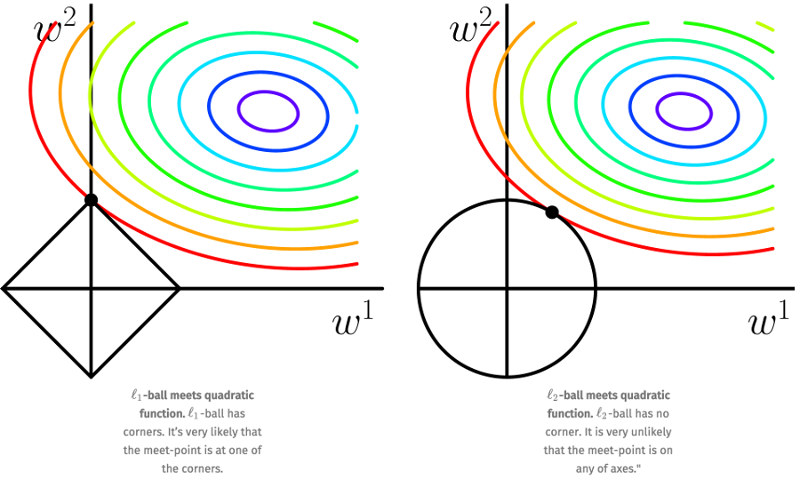
Figure 4: L1 VS L2 Regularization
可以看到,l1-ball 与 l2-ball 的不同在于它和每个坐标轴相交的地方都有“角”出现,而目标函数的测地线除非位置摆得非常好,大部分时候都会在角的地方相交。注意到在角的位置为产生稀疏性,例如图中的相交点就有 \(w^{(1)} = 0\) ,而更高维的时候(想象一下三维的 l1-ball 是什么样的?)除了角点以外,还有很多边的轮廓也是既有很大的概率成为第一次相交的地方,又会产生稀疏性。
相比之下,l2-ball 就没有这样的性质,因为没有角,所以第一次相交的地方出现在具有稀疏性的位置的概率就变得非常小了。这就从直观上来解释了为什么 L1 regularization 能产生稀疏性,而 L2 regularization 不易产生稀疏性的原因了。
参考:
Pattern Recognition and Machine Learning, 3.1.4 Regularized least squares
http://freemind.pluskid.org/machine-learning/sparsity-and-some-basics-of-l1-regularization
http://blog.csdn.net/zouxy09/article/details/24971995
4. 非线性情况
如何处理图 5 所示的分类呢?
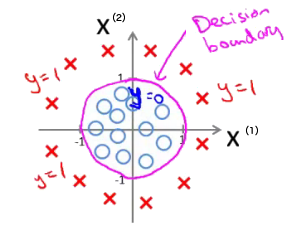
Figure 5: 非线性情况
尽管只有两个特征,我们可以 增加这两个特征的高阶式作为“新特征” ,如映射 \(x^{(3)} = {x^{(1)}}^2, x^{(4)} = {x^{(2)}}^2\)
这样令 \(z = \boldsymbol{w}^{\mathsf{T}} \boldsymbol{x} = w_0 + w_1 x^{(1)} + w_2 x^{(2)} + w_3 {x^{(1)}}^2 + w_4 {x^{(2)}}^2\) 。
如果求得 \(\boldsymbol{w} = (-1, 0, 0, 1, 1)\) ,即 \(z = -1 + {x^{(1)}}^2 + {x^{(2)}}^2\) ,这时可以使用这个模型预测当 \(-1 + {x^{(1)}}^2 + {x^{(2)}}^2 > 0\) 时,属于 \(y=1\) 的类别。
类似地,对于更加复杂的情况,我们可以增加“更高阶式”映射来处理。如图 6 所示。
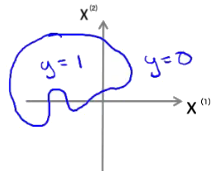
Figure 6: 可以增加“更高阶式”映射来处理
5. 多个分类情况
5.1. one vs. rest
默认 Logistic 回归仅输出两个分类。怎么让它处理多个分类的情况呢?可以采用“one vs. rest”方法(也称为“one vs. all”方法)。
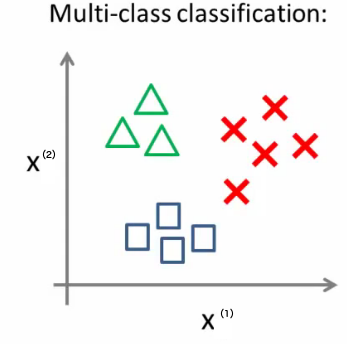
Figure 7: Multi-class 分类
“one vs. rest”方法的描述如下:
对每一个类分别训练出一个唯一的分类器,如图 7 所示的例子中我们一共可得到 3 个分类器,如图 8 所示。 对于输入数据,分别计算每一个分类器下的输出值,取“输出值最大的那个分类器对应的类别”作为预测类别。
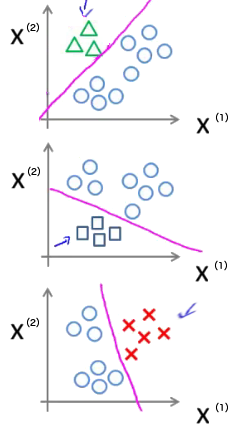
Figure 8: 对每一个类分别训练出一个唯一的分类器
参考:
https://en.wikipedia.org/wiki/Multiclass_classification
http://www.holehouse.org/mlclass/06_Logistic_Regression.html
5.2. Softmax 回归
Softmax 回归是 Logistic 回归模型在多分类问题上的推广。
参考:http://deeplearning.stanford.edu/wiki/index.php/Softmax%E5%9B%9E%E5%BD%92
6. Logistic 回归 VS 线性回归
线性回归假设各个特征和结果满足线性关系:
\[ y = b + w^{(1)} x^{(1)} + w^{(2)} x^{(2)} + \cdots + w^{(n)} x^{(n)} = \boldsymbol{w}^{\mathsf{T}} \boldsymbol{x}\]
其中, \(\boldsymbol{w}\) 是每个特征所占的权重。
说明:不满足线性关系也没关系,因为我们可以把特征映射到一个函数(如对某个特征求平方),然后再参与线性计算,这样特征与结果之间是非线性关系。
一般地,线性回归模型的输出是一个连续的值,如明天的温度是多少度、下月本市平均房价;而 Logistic 回归虽然是叫“回归”,其实本身是用来“分类”的,它的输出是 Categorical 值,如“true/false”、“明天会下雨/明天不会下雨”等等。
用线性回归也可以解决分类问题,指定一个阈值即可。例如,要测试明天温度是“冷/热”中哪一个,用线性回归预测具体温度后,使用一个阈值,既可划分为“冷/热”中的某一类了。
可以认为 Logistic 回归也包含线性回归过程,只是在特征到结果的映射中加入了一层函数映射,即先把特征线性求和,然后使用函数 \(\sigma(z) = \frac{1}{1+ e^{-z}}\) 将预测值映射到 0 和 1 上(注:可以认为 Logistic 回归这个名字来源就在于它的输出为 0 和 1)。
7. 再议 Logistic 回归损失函数
在 1.3 节中介绍过,给定的训练数据集 \(T = \{ (\boldsymbol{x_1}, y_1), (\boldsymbol{x_2}, y_2), \cdots, (\boldsymbol{x_N}, y_N)\}\) ,其中, \(\boldsymbol{x_i} \in \mathbb{R}^n, y_i \in \{0, 1\}\) 。则 Logistic 回归的损失函数为:
下面介绍一种上面损失函数的其它解释。
7.1. 交叉熵(Cross-Entropy)
在信息论中,设离散随机变量 \(X\) 的概率分布为 \(P(X=x^{(i)}) = p_i, \, i=1,2,\cdots,n\) ,则概率分布 \(p\) 的熵(Entropy)的定义为:
\[H(p) = - \sum_{i=1}^{n} p_i \log p_i\]
当熵定义中对数以 2 或以 \(e\) 为底时,熵的单位分别称为“比特(bit)”或者“纳特(nat)”。
关于同一组事件 \(x^{(1)}, \cdots, x^{(n)}\) 的两个分布 \(p,q\) ,其交叉熵(Cross-Entropy)的定义如下:
当两个分布完全相同时,交叉熵取最小值 \(H(p)\) 。 交叉熵可以衡量两个分布之间的相似度,交叉熵越小两个分布越相似。
下面是交叉熵的应用实例(例子摘自http://www.cs.rochester.edu/u/james/CSC248/Lec6.pdf)。
假设离散随机变量 \(X\) 有 4 个可能取值 \(A,B,C,D\) ,它的真实分布为 \(p\) ,它有两个近似的分布 \(q1,q2\) :
| \(A\) | \(B\) | \(C\) | \(D\) | |
|---|---|---|---|---|
| \(p\) | 0.4 | 0.1 | 0.25 | 0.25 |
| \(q1\) | 0.25 | 0.25 | 0.25 | 0.25 |
| \(q2\) | 0.4 | 0.1 | 0.1 | 0.4 |
求 \(H(p, q1), H(p, q2)\) (对数取 2 为底)。
\[\begin{aligned} H(p, q1) & = - \sum_{i=1}^{n} p_i \log q1_i \\
& = - (0.4 \cdot \log 0.25 + 0.1 \cdot \log 0.25 + 0.25 \cdot \log 0.25 + 0.25 \cdot \log 0.25) \\
& = 2 \\
H(p, q2) & = - \sum_{i=1}^{n} p_i \log q2_i \\
& = - (0.4 \cdot \log 0.4 + 0.1 \cdot \log 0.1 + 0.25 \cdot \log 0.1 + 0.25 \cdot \log 0.4) \\
& = 2.02 \\
\end{aligned}\]
由于 \(H(p, q1)\) 更小,我们可以认为分布 \(q1\) 比 \(q2\) 更接近真实分布 \(p\) 。
7.2. 交叉熵损失函数(Cross-Entropy Cost Function)
在 Logistic 回归中, \(y \in \{0, 1\}\) 是训练数据类标记,记 \(\hat{y} = \ln \pi(\boldsymbol{x})\) 为模型的输出。
记 \(p\) 为真实模型(样本数据给定的模型), \(q\) 是训练得到的模型。则有:
\[\begin{aligned} & p_{y=1} = y, \; p_{y=0} = 1 - y \\
& q_{y=1} = \hat{y}, \; q_{y=0} = 1 - \hat{y} \end{aligned}\]
我们可以使用交叉熵 \(H(p,q)\) 来度量 \(p\) 和 \(q\) 的相似度:
\[H(p,q) = - \sum_i p_i \log q_i = - [y \log \hat{y} + (1-y) \log (1- \hat{y})]\]
我们知道,交叉熵 \(H(p,q)\) 越小表明 \(p\) 和 \(q\) 越相似,当 \(p\) 和 \(q\) 完全相同时 \(H(p,q)\) 取最小值。所以 \(H(p,q)\) 可以作为“损失函数”。
设有 \(N\) 个训练数据,则所有训练数据的交叉熵之和为:
这和前文利用对数似然得到 Logistic 回归损失函数是一致的。Logistic 回归中, 对数似然损失(Log Likelihood Loss)函数就是交叉熵损失(Cross-Entropy Cost)函数。
参考:
https://en.wikipedia.org/wiki/Cross_entropy#Cross-entropy_error_function_and_logistic_regression