Multiparty Threshold ECDSA (GG18)
Table of Contents
1. 简介
本文讨论多个参与者如何共同完成 ECDSA 门限签名,主要讨论 2018 年 Rosario Gennaro 和 Steven Goldfeder 在论文 Fast Multiparty Threshold ECDSA with Fast Trustless Setup 中提出的方案,简称 GG18 方案。
2. Generic DSA signature
GG18 作者提出了一个通用的签名方案(G-DSA),它统一了 DSA 签名和 ECDSA 签名的表示方法。
G-DSA 如图 1 所示。其中 \(x\) 是私钥, \(k\) 随机产生, \(m\) 是待签名消息的哈希;而签名数据由 \(r,s\) 两部分组成。

Figure 1: Generic DSA
2.1. ECDSA 门限签名的难点
从前面介绍的标准 ECDSA 签名算法可知,签名中涉及了椭圆曲线上的乘法、加法、求逆等运算, 如何把这些运算改造为分布式方式是 ECDSA 门限签名的难点。
3. 主要思路
下面以 \((3,n)\) 门限为例,介绍一下 3 个参与者共同完成 ECDSA 签名的思路。首先把 ECDSA 签名算法中的随机数 \(k\) 拆成由 3 份相加组成 \(k=k_1 + k_2 + k_3\) ,把私钥 \(x\) 拆成由 3 份相加组成 \(x = w_1 + w_2 + w_3\) (详情参考节 4.2)。每个参与者 \(P_i\) 都只知道自己的那部分数据:
k_1, w_1 # 参与者 P_1 掌握,不泄露给别人 k_2, w_2 # 参与者 P_2 掌握,不泄露给别人 k_3, w_3 # 参与者 P_3 掌握,不泄露给别人
再想方设法去构造签名数据 \(r,s\) 。
3.1. 求签名中的 r
只要计算出 \(R\) ,就容易求出 \(r\) 。下面介绍一下求 \(R = g^{k^{-1}}\) 的思路:
\[\begin{aligned}
R &= g^{k^{-1}} \\
&= g^{\gamma k^{-1} \gamma^{-1}} \\
&= g^{\left(\sum \gamma_i \right) k^{-1} \gamma^{-1}} \\
&= \left( g^{(\sum \gamma_i)} \right)^{(k \gamma)^{-1}} \\
&= \left( \prod g^{\gamma_i} \right)^{(k \gamma)^{-1}}
\end{aligned}\]
求 \(R\) 的思路是:
- 引入一个变量 \(\gamma\) ,同样由 3 份(每份由参与者 \(P_i\) 自己随机生成)相加组成 \(\gamma = \gamma_1 + \gamma_2 + \gamma_3\) ,每个参与者单独计算 \(g^{\gamma_i}\) ,这个是可以公开的,因为由 \(g^{\gamma_i}\) 反推不出 \(\gamma_i\) ,这样,大家就可以算出 \(\prod g^{\gamma_i}\) 了。
- 那如何求解 \(k \gamma = (\sum{k_i})(\sum{\gamma_i})\) 呢?每个参与者 \(P_i\) 手里只有 \(k_i, \gamma_i\) ,且需要保证这两个值的机密,如何一起配合求得 \((\sum{k_i})(\sum{\gamma_i})\) 呢?使用一种技巧可以实现,把 \(k \gamma\) 拆分为 3 份之和,即 \(k \gamma = \delta_1 + \delta_2 + \delta_3\) ,每个参与者 \(P_i\) 计算 \(\delta_i\) ,并公开 \(\delta_i\) 给其它参与者,这不会泄密 \(k_i, \gamma_i\) ,这样每个参与者都可以计算 \(k \gamma\) 了 ,其详情可参考节 4.2.2.1。
有了上面这两个信息, \(R\) 就可以计算出来了,从而 \(r\) 也可以计算出来了。
3.2. 求签名中的 s
签名中的另一部分 \(s= k (m + x r)\) ,其中 \(m\) 是消息的哈希, \(x\) 是私钥, \(r\) 在上一节已经求得了。下面介绍一下求 \(s\) 的思路 :
\[\begin{aligned}
s &= k (m + x r) \\
&= (k_1 + k_2 + k_3)m + kxr \\
&= (k_1 + k_2 + k_3)m + (\sigma_1 + \sigma_2 + \sigma_3) r \\
&= (m k_1 + r \sigma_1) + (m k_2 + r \sigma_2) + (m k_3 + r \sigma_3) \\
\end{aligned}\]
求 \(s\) 的主要思路是使用一种技巧把 \(kx\) 拆分为 3 份之和(至于怎么拆分可参考节 4.2.2.2,其实这和上一节求解 \(k\gamma\) 时,把 \(k\gamma\) 拆分为 3 份之和的原理是一样的),即 \(kx = \sigma_1 + \sigma_2 + \sigma_3\) ,每个参与者 \(P_i\) 单独计算自己的那个 \(s_i = mk_i + r \sigma_i\) ,并公开给其它参与者,这样每个参与者就都可以得到 \(s=s_1+s_2+s_3\) 了。
4. 协议描述
下面仅描述 GG18 协议的“核心思想”,有细节省略。
4.1. Distributed Key Generation
假设系统中有 4 个参与者(Alice/Bob/Carol/Dave),其中任意 3 个人可以完成签名,而少于 3 个人无法签名。
下面介绍一个 Distributed Key Generation 流程:
1、每个参与者 \(P_i\) 随机选择一个 \(u_i\) ,这就是每个参与者自己的秘密值,需要各参与者自己保存好。假设 Alice/Bob/Carol/Dave 分别选择了:
u_1 = 120 u_2 = 10 u_3 = 30 u_4 = 80
整体的秘密(私钥)就是 \(x = \sum u_i = u_1 + u_2 + u_3 + u_4 = 120 + 10 + 30 + 80 = 240\) ,每个参与者都不知道这个秘密值,下面将在不引入 Trusted Dealer 的情况下,把秘密值 \(x=240\) 以 \((3,4)\) 门限的方式分散给 Alice/Bob/Carol/Dave。
2、每个参与者 \(P_i\) 把自己的秘密值 \(u_i\) 通过 \((t, n)\) Feldman-VSS 分享给其它所有参与者。每个参与者把自己收到的所有分享全部加起来得到 \(x_i\) ,容易知道 \(x_i\) 是 \(x\) 的 \((t,n)\) 分享。比如,Alice 选择一个 2 次多项式 \(f_a(x) = 3 x^2 - 10x + u_1 = 3 x^2 - 10x + 120\) 把 120 分享给所有参与者,计算:
f_a(1) = 113 # Alice 自己留着 f_a(2) = 112 # 发送给 Bob f_a(3) = 117 # 发送给 Carol f_a(4) = 128 # 发送给 Dave
类似地,Bob 选择一个 2 次多项式 \(f_b(x) = 6 x^2 + x + u_2 = 6 x^2 + x + 10\) 把 10 分享给所有参与者,计算:
f_b(1) = 17 # 发送给Alice f_b(2) = 36 # Bob 自己留着 f_b(3) = 67 # 发送给 Carol f_b(4) = 110 # 发送给 Dave
Carol 选择一个 2 次多项式 \(f_c(x) = 7 x^2 - x + u_3 = 7 x^2 - x + 30\) 把 30 分享给所有参与者,计算:
f_c(1) = 36 # 发送给 Alice f_c(2) = 56 # 发送给 Bob f_c(3) = 90 # Carol 自己留着 f_c(4) = 138 # 发送给 Dave
Dave 选择一个 2 次多项式 \(f_d(x) = x^2 + 2x + u_4 = x^2 + 2x + 80\) 把 80 分享给所有参与者,计算:
f_d(1) = 83 # 发送给 Alice f_d(2) = 88 # 发送给 Bob f_d(3) = 95 # 发送给 Carol f_d(4) = 104 # Dave 自己留着
然后,Alice/Bob/Carol/Dave 分别计算他们的 \(x_i\) ,这就是他们各个的密钥分片,需要各个保存好:
x_1 = f_a(1) + f_b(1) + f_c(1) + f_d(1) = 113+17+36+83 = 249 # Alice 计算并保存 x_2 = f_a(2) + f_b(2) + f_c(2) + f_d(2) = 112+36+56+88 = 292 # Bob 计算并保存 x_3 = f_a(3) + f_b(3) + f_c(3) + f_d(3) = 117+67+90+95 = 369 # Carol 计算并保存 x_4 = f_a(4) + f_b(4) + f_c(4) + f_d(4) = 128+110+138+104 = 480 # Dave 计算并保存
至此, 私钥 240 已经通过 \((3,4)\) 门限的方式分散到了 Alice/Bob/Carol/Dave 4 个参与者中,也就是说 \((1, 249), (2, 292), (3, 369), (4, 480)\) 这 4 个点中任意找 3 个点通过拉格朗日插值得到的多项式,它在 0 处的值就是秘密值 240, 如图 2 所示。
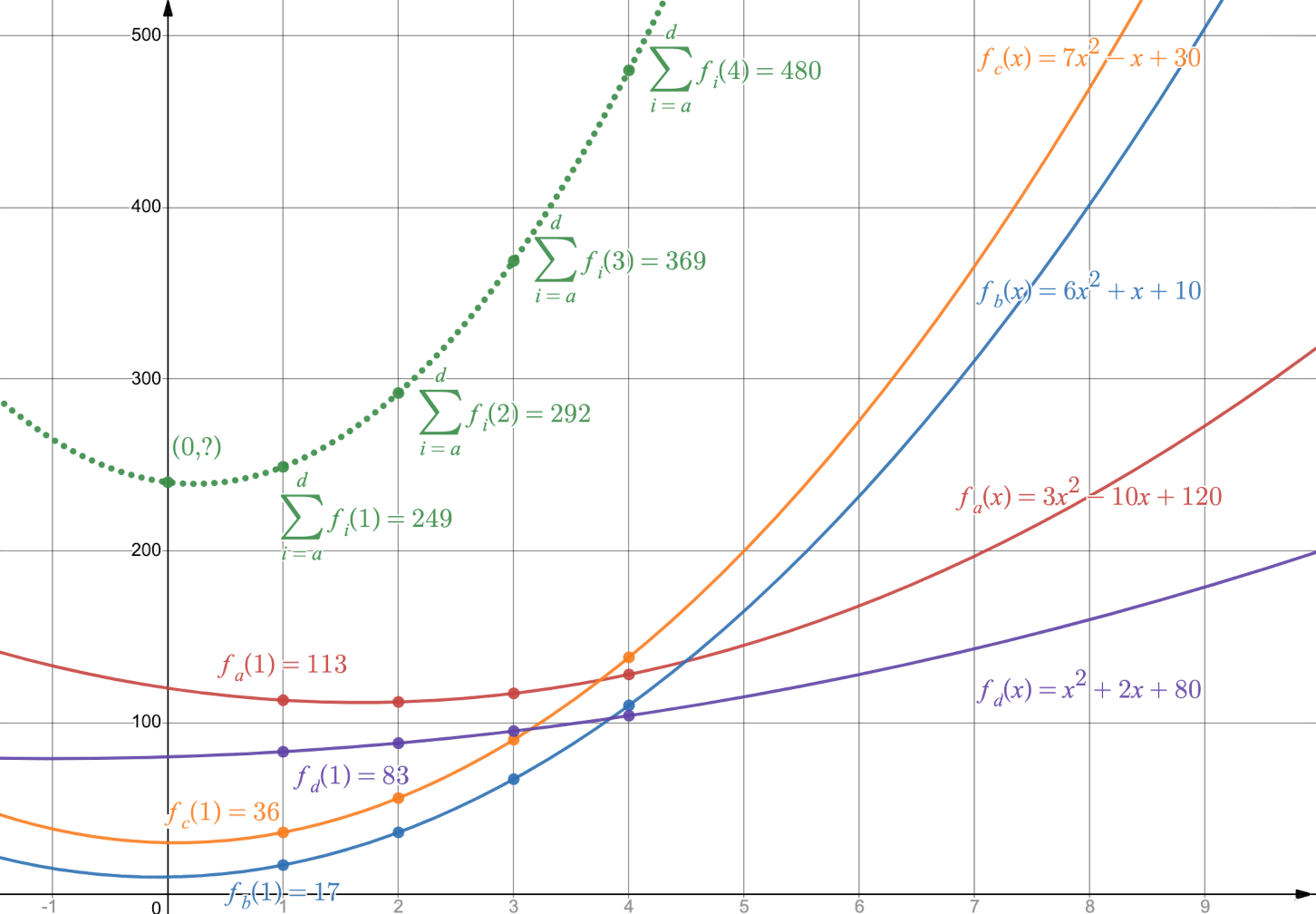
Figure 2: Key Generation。这 4 个点 \((1, 249), (2, 292), (3, 369), (4, 480)\) 在一个 2 次多项式上(绿色虚线所示),这个曲线(2 次多项式)是由 4 个参与者各自的曲线(2 次多项式)相加而成。显然 0 处的值等于 \(f_a(0)+f_b(0)+f_c(0)+f_d(0)=120+10+30+80=240\)
可以把上面过程看作是一种“不需要 Trusted Dealer 的 Shamir秘密分享”。
上面介绍了如何把私钥(即 240)分散保存到 4 个参与者中。但如何在不知道 240 这个私钥的情况下,各参与者得到公钥呢?其实很简单,每个参者与公开自己的 \(u_i * G\) (这并不会导致 \(u_i\) 泄露),公钥就是:
y = u_1 * G + u_2 * G + u_3 * G + u_4 * G = (u_1 + u_2 + u_3 + u_4) * G
上面描述的 DKG 过程是 1991 年 Pedersen 在论文 A Threshold Cryptosystem without a Trusted Party 中提出的,可称为 Pedersen's DKG(又可称为 Joint Feldman DKG,或者简称 JF DKG)。
不过,1999 年,Rosario Gennaro, Stanislaw Jarecki, Hugo Krawczyk, and Tal Rabin 在论文 Secure Distributed Key Generation for Discrete-Log Based Cryptosystems 中指出 Pedersen's DKG(Joint Feldman DKG)不是安全的,具体来说就是:如果 Pedersen's DKG(Joint Feldman DKG)过程中攻击者控制了 2 个参与者(共 \(n\) 个参与者),那攻击者可以使私钥的分布不再是均匀分布。后来在 2003 年,Rosario Gennaro, Stanislaw Jarecki, Hugo Krawczyk, and Tal Rabin 在论文 Secure Applications of Pedersen’s Distributed Key Generation Protocol 中指出,Pedersen's DKG(Joint Feldman DKG)在某些场景下也足够安全。
GG18 中的 DKG 算法是在 Pedersen's DKG(Joint Feldman DKG)的基础上增加了零知识证明来确保各个参与者按照协议规定的方式运行。
4.1.1. DKG 总结
论文对 DKG 的描述如图 3 所示。

Figure 3: GG18 DKG(没有包含 MtA 子协议中 Range Proof 所需要的参数)
GG18 DKG 包含 2 部分内容:
- 各个参与者通过 Pedersen's DKG(Joint Feldman DKG)协议(图 3 中黄色下划线部分)得到 \(x_i\) ,它是完整私钥 \(x\) 的 Shamir 分片, \(g^{x_i}\) 公开给别人。需要通过零知识证明,参与者不泄露 \(x_i\) 的情况下证明他确实知道 \(x_i\) (图 3 中绿色下划线部分)。
- 各个参与者生成一个 Paillier 公钥(图 3 中蓝色下划线部分)发送给别人(签名过程中 MtA 子协议会用到 Paillier 同态加密,在 DKG 过程中需要提前分发 Paillier 公钥)。需要通过零知识证明,参与者不泄露 Paillier 公钥所对应的私钥的情况下证明他确实知道 Paillier 的私钥。不过,GG18 中并没有要求这一点,只在图 3 中红色下划线处要求 Paillier 公钥 \(N_i\) 是一个 Square-free 整数(不包含平方因子的整数),也就是说 GG18 协议只要求 Paillier 公钥 \(N_i\) 不包含平方因子。比如,对于 \(N_i\) 有多个素因子的情况 \(N_i = p_1 p_2 p_3 \cdots p_n\) ,GG18 并不能检测这种情况。 GG18 没有严格地校验 Paillier 公钥 \(N_i\) 的合法性(即 \(N_i\) 必须是两个较大的安全素数的乘积),这导致了 GG18 出现了安全漏洞 CVE-2023-33241。 关于这个安全漏洞的细节可参考节 8.3。
上面过程涉及的零知识证明有:
- 如何不泄露 \(x_i\) 情况下证明他确实知道公钥 \(g^{x_i}\) 背后的私钥 \(x_i\) 呢?可以采用 Schnorr’s protocol。
- 如何不泄露 Paillier 私钥的情况下证明他确实知道 Paillier 公钥 \(N_i\) 背后的私钥(素数 \(p_i,q_i\) )呢?需要证明 \(N_i\) 确实是两个安全素数 \(p_i,q_i\) 的乘积,且这两个安全素数确实满足 Paillier 私钥的要求,即 \(p_iq_i\) 和 \((p_i-1)(q_i-1)\) 互素,关于这个零知识证明协议可以参考 UC Non-Interactive, Proactive, Threshold ECDSA (CMP) 的 4.3 节 Paillier-Blum Modulus ZK。为了更好的安全性,我们还要通过零知识证明协议证明 \(N_i\) 没有小的素因子,即 \(p_i,q_i\) 都是比较大的素数,关于这个零知识证明协议可以参考 UC Non-Interactive, Proactive, Threshold ECDSA (CMP) 的 B.4 节 No Small Factor Proof。
注 1:GG18 签名过程中有个 MtA 子协议,它需要 Range Proof,GG18 中提到为了性能考虑可以省略 Range Proof,不过为了更好的安全论文中建议实现 Range Proof。有的 GG18 实现(如 Binance 的实现)包含了 Range Proof,而有的 GG18 实现(ZenGo 的实现)则没有包含 Range Proof。进一步的研究表明,没有 Range Proof 会导致私钥泄露,参考节 8.1.2。如果要包含 Range Proof,则 DKG 过程除图 3 描述的步骤外,还需要准备额外的一些参数,参考节 8.1.2。
注 2:零知识证明是必不可少,否则会导致完整私钥泄露,这里有个省略零知识证明造成私钥泄露的例子:https://www.fireblocks.com/blog/bitgo-wallet-zero-proof-vulnerability/
4.2. Signature Generation
现在,Alice/Bob/Carol 这 3 个人想要进行签名,他们手头的“部分秘密”分别为 249,292,369。它们是整体秘密 \(x=240\) 的 \((3, 4)\) Feldman-VSS 分享方案,我们先求得整体秘密(即 \(x=240\) )的 3 人 Additive Sharing 分享方案。即求 \(w_1, w_2, w_3\) ,且满足 \(w_1 + w_2 + w_3 = 240\) ,其细节可参考节 8.2,这里直接给出答案:
w_1 = 747 w_2 = -876 w_3 = 369
4.2.1. Phase 1
Alice/Bob/Carol 选择 \(k_i, \gamma_i\) ,例如:
k_1 = 30 # Alice 随机选择 k_2 = 41 # Bob 随机选择 k_3 = 25 # Carol 随机选择 γ_1 = 19 # Alice 随机选择 γ_2 = 8 # Bob 随机选择 γ_3 = 16 # Carol 随机选择
定义 \(k \triangleq \sum k_i = 30 + 41 + 25 = 96\) ,定义 \(\gamma \triangleq \sum \gamma_i = 19 + 8 + 16 = 43\)
4.2.2. Phase 2
每两个人都进行两次 MtA 协议(参考节 8.1),具体介绍如下。
4.2.2.1. 第一次 MtA 协议(为求 kγ 做准备)
第一次 MtA 协议: \(P_i,P_j\) 对 \(k_i,\gamma_j\) 使用 MtA,把 \(P_i\) 得到的结果记为 \(\alpha_{ij}\) , \(P_j\) 得到的结果记为 \(\beta_{ij}\) ,也就是满足 \[k_i \gamma_j = \alpha_{ij} + \beta_{ij}\]
具体演示(下面的 \(\alpha_{ij}, \beta_{ij}\) 的值是满足要求情况下随意写的)如下:
k_1 * γ_2 = α_{12} + β_{12} => 30 * 8 = 100 + 140
k_1 * γ_3 = α_{13} + β_{13} => 30 * 16 = 120 + 360
k_2 * γ_1 = α_{21} + β_{21} => 41 * 19 = 80 + 699
k_2 * γ_3 = α_{23} + β_{23} => 41 * 16 = 117 + 539
k_3 * γ_1 = α_{31} + β_{31} => 25 * 19 = 218 + 257
k_3 * γ_2 = α_{32} + β_{32} => 25 * 8 = 30 + 170
定义 \(\delta_i \triangleq k_i \gamma_i + \sum_{j \neq i} \alpha_{ij} + \sum_{j \neq i} \beta_{ji}\) ,则:
\[\begin{aligned}
\delta_1 &= k_1 \gamma_1 + \alpha_{12} + \alpha_{13} + \beta_{21} + \beta_{31} \\
&= 30 * 19 + 100 + 120 + 699 + 257 \\
&= 1746 \\
\delta_2 &= k_2 \gamma_2 + \alpha_{21} + \alpha_{23} + \beta_{12} + \beta_{32} \\
&= 41 * 8 + 80 + 117 + 140 + 170 \\
&= 835 \\
\delta_3 &= k_3 \gamma_3 + \alpha_{31} + \alpha_{32} + \beta_{13} + \beta_{23} \\
&= 25 * 16 + 218 + 30 + 360 + 539 \\
&= 1547 \\
\end{aligned}\]
可以推出 \(k \gamma = \left( \sum k_i \right) \cdot \left( \sum \gamma_i \right)= \sum \delta_i\) 。
Alice (即 \(P_1\) )公开 \(\delta_1\) 给 Bob 和 Carol;而 Bob (即 \(P_2\) )公开 \(\delta_2\) 给 Alice 和 Bob;Carol (即 \(P_3\) )公开 \(\delta_3\) 给 Alice 和 Bob。这样,Alice/Bob/Carol 在不公开自己拥有的 \(k_i, \gamma_i\) 的情况下,都可以计算出 \(k \gamma\) 了。
4.2.2.2. 第二次 MtA 协议(为求 s_i 做准备)
第二次 MtA 协议: \(P_i,P_j\) 对 \(k_i,w_j\) 使用 MtA,把 \(P_i\) 得到的结果记为 \(\mu_{ij}\) , \(P_j\) 得到的结果记为 \(\nu_{ij}\) ,也就是满足 \[k_i w_j = \mu_{ij} + \nu_{ij}\]
具体演示(下面的 \(\mu_{ij}, \nu_{ij}\) 的值是满足要求情况下随意写的)如下:
k_1 * w_2 = μ_{12} + ν_{12} => 30 * (-876) = -51000 + 24720
k_1 * w_3 = μ_{13} + ν_{13} => 30 * 369 = 4000 + 7070
k_2 * w_1 = μ_{21} + ν_{21} => 41 * 747 = 21452 + 9175
k_2 * w_3 = μ_{23} + ν_{23} => 41 * 369 = 3413 + 11716
k_3 * w_1 = μ_{31} + ν_{31} => 25 * 747 = 14737 + 3938
k_3 * w_2 = μ_{32} + ν_{32} => 25 * (-876) = -30000 + 8100
定义 \(\sigma_i \triangleq k_i w_i + \sum_{j \neq i} \mu_{ij} + \sum_{j \neq i} \nu_{ji}\) ,则:
可以推出 \(k x = \left( \sum k_i \right) \cdot \left( \sum w_i \right)= \sum \sigma_i\) 。
4.2.3. Phase 3(求 r)
Alice/Bob/Carol 公开 \(\delta_i\) ,这样,所有参与者都可以计算出 \(k \gamma=\sum \delta_i = 1746 + 835 + 1547 = 4128\) , \(k \gamma\) 是求 \(r\) 所需要计算的东西,参考节 3.1 。
4.2.4. Phase 4(求 r)
Alice/Bob/Carol 公开 \(g^\gamma_i\) ,这样可以求得 \(R\) ,从而求得 \(r\) 了,参考节 3.1 。
4.2.5. Phase 5(求 s)
在第二次 MtA 协议后,Alice/Bob/Carol 各自计算出了 \(\sigma_i\) ,从而各自可以计算出 \(s_i \triangleq mk_i + r \sigma_i\) ,再公开(不是直接公开,还有一些防止别人做恶的手段,这里省略)给大家,这样大家就可以求得 \(s=s_1+s_2+s_3\) 了,参考节 3.2 。
5. GG18 VS. GG20
Rosario Gennaro 和 Steven Goldfeder 于 2020 年发表论文 One Round Threshold ECDSA with Identifiable Abort,被称为 GG20。它比 GG18 更优秀:
- Rounds 数量更少;GG18 的 sign 过程需要 9 rounds,而 GG20 的 sign 过程只需要 7 rounds(前 6 个 rounds 和待签名的 msg 无关,可提前进行;最后一个 round 才和 msg 相关)。
- 可识别恶意参与者。GG18 协议,如果有恶意参与者,那么协议会终止,但在某些场景下却不知道谁是恶意参与者。在 GG20 协议中,只要协议失败,就可识别出是谁的责任。
6. 开源实现
GG18, GG20 的开源实现可以参考:
- https://github.com/bnb-chain/tss-lib GG18 实现
- https://gitlab.com/thorchain/tss/tss-lib GG20 实现
- https://github.com/ZenGo-X/multi-party-ecdsa GG18 和 GG20 实现
7. 扩展阅读
7.1. Resharing(动态改变门限 t)
Distributed Key Generation 结束后,门限 \(t\) 就确定了,以后还可以改变吗?比如从 \((3,4)\) 改为新门限设置 \((5,7)\) ?答案是肯定的,不过在 GG18 论文中没有提到这一点。
具体做法是分两步:
- 从 \((3,4)\) 变为 3 人 Additive Sharing(如 \(w_1,w_2,w_3\) ),参考节 8.2 ;
- 把 3 人的 Additive Sharing 当作是 DKG(参考节 4.1)过程中的随机数 \(u_i\) (由于新门限的 \(n\) 值是 7,设置多出来的 4 个新参与者其 \(u_i=0\) 即可,也就是说 \(\underbrace{u_i}_{i=1,2,3}=w_i,\underbrace{u_i}_{i=4,5,6,7}=0\) ),再接着运行 DKG 即可得到新门限设置 \((5,7)\) 的 DKG 结果。
在论文 Attacking Threshold Wallets 的 3.1 节中介绍了这个过程。
注:上面的第 2 步也可以采用其它方案,比如让 3 个旧参与者 \(P_1,P_2,P_3\) 把他们的 Additive Sharing 拆分为 5 份,自己留一份,4 个新参与者 \(P_4,P_5,P_6,P_7\) 每人一份,比如旧参与者 \(P_1\) 把 \(w_1\) 变为 5 个值 \(r_{14},r_{15},r_{16},r_{17},w_1 - (r_{14}+r_{15}+r_{16}+r_{17})\) 之和,其中 \(r_{1j}\) 是 \(P_1\) 随机产生的,需要通过加密通道发送给新参与者 \(P_j\) ;新参与者,如 \(P_4\) ,把从 \(P_1,P_2,P_3\) 发送来的值解密后(即 \(r_{14},r_{24},r_{34}\) )相加作为自己的 \(u_i\) 。这样, \[\begin{aligned} u_1 &= w_1 - (r_{14}+r_{15}+r_{16}+r_{17}) \\ u_2 &= w_2 - (r_{24}+r_{25}+r_{26}+r_{27}) \\ u_3 &= w_3 - (r_{34}+r_{35}+r_{36}+r_{37}) \\ u_4 &= r_{14} + r_{24} + r_{34} \\ u_5 &= r_{15} + r_{25} + r_{35} \\ u_6 &= r_{16} + r_{26} + r_{36} \\ u_7 &= r_{17} + r_{27} + r_{37} \end{aligned}\] 显然这也会满足 \(\sum_{i=1}^{7} u_i = w_1+w_2+w_3\) ,从而 Resharing 后,背后的整体私钥不会变。
7.2. 其它 ECDSA 门限签名算法
除 GG18/GG20 外,还有其它一些 ECDSA 门限签名算法,可参考:A Survey of ECDSA Threshold Signing
7.2.1. CCLST
2020 年,Guilhem Castagnos, Dario Catalano, Fabien Laguillaumie, Federico Savasta, and Ida Tucker 于在论文 Bandwidth-efficient Threshold EC-DSA 中提出了一种门限签名 ECDSA 算法,一般称为 CCLST。
CCLST 可以看作是 GG18 的变种,它和 GG18 的主要区别是:MtA 协议中使用的同态加密算法不一样,GG18 是使用 Paillier 同态加密算法,而 CCLST 是使用 CL Scheme 同态加密算法。 这样做的好处是: 使用 CL Scheme 同态加密算时,不再需要耗时的 Range Proof,因为 CL Scheme 的明文消息空间和椭圆曲线的 Order 是一样的。 注:使用 Paillier 同态加密时,之所以需要 Range Proof,就是由于明文消息空间(即 \(N\) )和椭圆曲线的 Order(即 \(q\) )可能不一样,详情参见节 8.1.1。
7.3. 和 RFC 6979 不兼容
RFC 6979 定义了一种确定性 \(k\) 的方案,在这个方案中, \(k\) 由私钥和待签名消息来确定, \(k\) 不再是随机的,从而对一个消息进行多次签名,得到的签名结果是一样的。在 GG18 中,每次签名时使用的 \(k\) 都是随机的,从而对一个消息进行多次签名,每次的签名结果都不一样。
7.4. 对 BIP32 的支持
BIP32 有两种推导方式:Normal (Non-Hardened) Derivation 和 Hardened Derivation。
对于 Normal Derivation 来说,推导子地址时,不需要访问父私钥;而对于 Hardened Derivation 来说,推导子地址时,需要访问父私钥。由于在门限方案中完整私钥是不存在于某个单点的,这导致门限钱包支持 Hardened Derivation 要麻烦很多。这里仅介绍一下门限钱包如何支持 Normal Derivation。
门限钱包支持 BIP32 Normal Derivation 的思路如下:
- 在 Keygen 过程中,各个参与者要协商(后面会介绍具体步骤)出一个共同的 Chain Code,作为 Master Chain Code。
- 有了 Master Chain Code 后,又因为整体公钥是公开的,各个参与者可以本地计算出子私钥和父私钥的偏移量 Delta 及新的 Chain Code。具体方法是把 HMAC-SHA512(Key=Chain Code, Data=parent_pubkey||index) 的左 256 比特位作为 Delta,而右 256 比特位作为新的 Chain Code。
- 有了 Delta 后,各个参与者可以利用本地的父 Key Share 创建新的子 Key Share。这里是进行 Normal Derivation,并不需要 MPC 过程。具体方法如下:假设 \((2,3)\) 门限方案 Keygen 结束后,3 个参与者本地保存的父 Key Share 和其它数据为:
# 3 个参与者的父 Key Share Party 1: keyshare private data: f(1) keyshare public data: [f(2) G, f(3) G] other data: Paillier related data, etc Party 2: keyshare private data: f(2) keyshare public data: [f(1) G, f(3) G] other data: Paillier related data, etc Party 3: keyshare private data: f(3) keyshare public data: [f(1) G, f(2) G] other data: Paillier related data, etc
当我们要推导一个子地址时,通过前面步骤已经计算出了 Delta,则各个参与者可以通过下面方式本地生成 Child Key Share:
# 3 个参与者的子 Key Share(Normal Derivation) Party 1: keyshare private data: f(1) + delta keyshare public data: [f(2) G + delta G, f(3) G + delta G] other data: Paillier related data, etc Party 2: private data: f(2) + delta public data: [f(1) G + delta G, f(3) G + delta G] other data: Paillier related data, etc Party 3: private data: f(3) + delta public data: [f(1) G + delta G, f(2) G + delta G] other data: Paillier related data, etc
参与者也并不需要保存这个 Child Key Share,只用保存最原始的 Master Chain Code,需要 Child Key Share 时,实时生成即可。
7.4.1. 生成 Master Chain Code
前面提到参与者要协商出一个共同的 Master Chain Code。这要如何做到呢?可以用下面简单的思路:
- 各个参与者本地生成一个 Chain Code i,然后把它的 Commitent 发送给其它参与者;
- 收到其它参与者发来的 Commitent 以后,才把自己的 Chain Code i 发送给其它参与者;
- 收到其它参与者发来的 Chain Code i,校验是否和之前收到的 Commitent 一致,如果一致则最终的 Chain Code 等于所有收到的 Chain Code i 及自己的那个 Chain Code 的异或。
注:为什么要收到所有其它人发来的 Commitent 后,才公布自己的 Chain Code i 呢?这是为了避免某个参与者根据其它人传来的 Chain Code i 来调整自己的 Chain Code i,从而这个参与者可以完全地决定最终的 Chain Code。
门限钱包支持 BIP32 Normal Derivation 的实现可参考:taurusgroup 库 multi-party-sig。
8. Appendix
8.1. Multiplicative-to-Additive(MtA)协议
假设 Alice 有个秘密值 \(a \in \mathbb{Z}_q\) ,而 Bob 有个秘密值 \(b \in \mathbb{Z}_q\) ,下面介绍一个协议可以在 Alice 不泄露 \(a\) ,Bob 不泄露 \(b\) 的情况下,Alice 和 Bob 分别得到另外一个秘密值 \(\alpha \in \mathbb{Z}_q,\beta \in \mathbb{Z}_q\) ,满足: \[ab = \alpha+\beta \bmod q\] 这个协议称为乘法到加法的转换协议(MtA)。
图 4 是 MtA 协议的示意图,协议中用到了 Paillier 同态加密。
Figure 4: Multiplicative-to-Additive(MtA)协议的示意图
Alice 把 \(a\) 使用 Alice 公钥进行加密后,给 Bob;而 Bob 利用 Paillier 同态加密性质,把加密(当然也是 Alice 公钥加密)后的 \(ab-\beta\) 给 Alice。这样 Alice 使用私钥解密后得到的值记为 \(\alpha\) ,它们会满足 \(ab = \alpha+\beta \bmod q\) (注:这里不是很严谨,Paillier 解密后得到的值是 \(ab - \beta \bmod N\) ,而 MtA 协议要求的是对 \(q\) 取模,下一节会介绍当 \(ab - \beta < N\) 时,对 \(q\) 取模也一样成立)。
8.1.1. MtA 完整描述
前面图 4 仅仅是 MtA 协议的示意图,完整的 MtA 协议如图 5 所示。
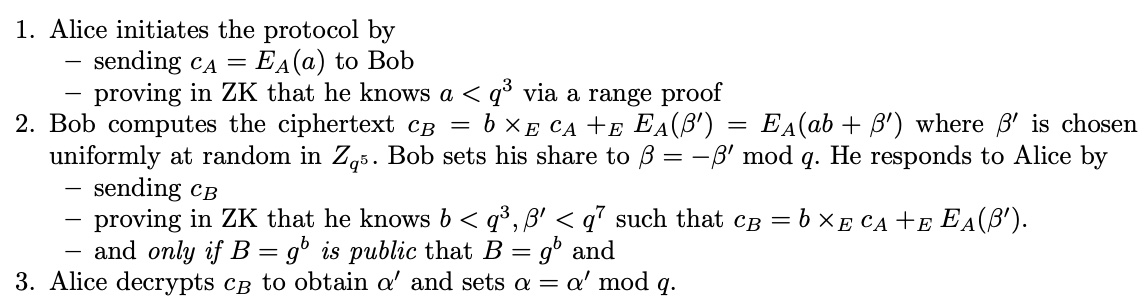
Figure 5: Multiplicative-to-Additive(MtA)协议
图 5 和前面示意图 4 的一个明显不同是图 5 中加入了 Range Proof,下面介绍为什么需要它。
MtA 协议中使用了 Paillier 同态加密,Alice 和 Bob 的 Paillier 公钥在 Key Generation 阶段就已经传给了对方。Paillier 加密算法要求待加密的明文必须小于 Paillier 公钥 \(N\) (Paillier 解密算法最后有个 \(\bmod N\) 运算,这要求待加密的明文不能超过 \(N\) )。MtA 协议中,Bob 会使用 Paillier 加密算法加密 \(ab + \beta'\) 后,发送给 Alice。Alice 解密后得到的值记为 \(\alpha'\) ,有 \(\alpha' = ab + \beta' \bmod N\) 。
如果 \(ab + \beta' < N\) ,那么 \(\bmod N\) 运算没有执行可以直接去掉,也就是说有 \(\alpha' = ab + \beta'\) ,从而 \(\alpha \triangleq \alpha' \bmod q = ab + \beta' \bmod q\) 。这时, \(\alpha\) 满足 MtA 的要求。
如果 \(ab + \beta' >= N\) ,那么 \(\bmod N\) 运算被执行了,从而 \(\alpha \triangleq \alpha' \bmod q = (ab + \beta' \bmod N) \bmod q\) 。这时, \(\alpha\) 并不满足 MtA 的要求。
也就是说: 为了使 MtA 协议成立, \(ab + \beta' < N\) 是必须满足的。
怎样才能保证 \(ab + \beta' < N\) 成立呢?GG 18 采用的办法是:让 \(a,b,\beta'\) 不能太大,而 \(N\) 不能太小。具体来说,在 Key Generation 阶段收到别人 Paillier 公钥 \(N\) 时,检查 \(N > q^8\) 是否满足,不满足报错;Alice 通过 Range Proofs 保证 \(a < q^3\) ,而 Bob 通过 Range Proof 保证 \(b < q^3, \beta' < q^7\) 。这个设置显然能保证 \(ab + \beta' < N\) 成立,因为 \(q^3 q^3 + q^7\) 肯定会小于 \(q^8\) 。这就是 MtA 协议中需要 Range Proof 的原因。
在区块链实践中, \(q\) 是 Secp256k1 的 order,它是 256 比特位长度;而 \(N\) 是 2048 比特位长度。
8.1.2. Range Proof
前面介绍了为什么使用 Paillier 同态加密的 MtA 协议中需要 Range Proof。那如何实现 Paillier 密文的 Range Proof 呢?也就是说 Prover 发给 Verifier 一个 Paillier 密文, Prover 在不泄露明文的情况下如何向 Verifier 证明这个 Paillier 密文对应的明文会属于某个整数范围中。
GG18 A.1 Range Proof 中给出了完整的 Range Proof 协议,这个协议并不是 Rosario Gennaro 和 Steven Goldfeder 原创的,而是来源于 Two-party generation of DSA signatures ,6.3 Proof \(\Pi\) 。论文 UC Non-Interactive, Proactive, Threshold ECDSA,1.2.6 Non-Interactive Zero-Knowledge 节对这个 Range Proof 进行了更加详细的描述。
这里不介绍 Range Proof 协议的细节。需要指出:在执行 Range Proof 协议时,Prover 需要准备好 Paillier 公钥 \(N\) ,发送给 Verifier;而 Verifier 需要准备好 3 个参数 \(\tilde{N}, h_1, h_2\) ,发送给 Prover。这些参数都需要在 Key Generation 过程中准备好,如果 GG18 实现中包含了 Range Proof,则在 DKG 过程(节 4.1.1)中需要增加 \(\tilde{N}, h_1, h_2\) 的创建和验证步骤(对于 \(\tilde{N}, h_1, h_2\) 创建和验证相关的实现源码可参考 dln_proof in Safeheron crypto-zkp-cpp 和 dln proof in Binance tss-lib)。
MtA 协议中省略 Range Proof 会造成完整私钥的泄露,相关攻击可参考论文:Alpha-Rays: Key Extraction Attacks on Threshold ECDSA Implementations, 2.2 Attack on absent range proofs(文中提到了 8 次签名能盗走私钥的方法)。
8.2. 转换 (t,n) 秘密为 Additive Sharing
Alice/Bob/Carol 手头分别有部分秘密 \(x_1=249, x_2=292, x_3=369\) ,它们是整体秘密 \(x=240\) 的 \((3, 4)\) Feldman-VSS 分享方案,现在想把它变为整体秘密 \(x=240\) 的 3 人 additive sharing 分享方案。也就是 Alice/Bob/Carol 通过计算分别得到另外一个部分秘密 \(w_1,w_2,w_3\) ,要满足 \(w_1 + w_2 + w_3 = 240\) 。
具体来说, \(w_i\) 可以通过拉格朗日系数乘以 \(x_i\) 得到:
\[\begin{aligned}
w_1 &= \lambda_1 \cdot x_1 = \frac{0-2}{1-2} \cdot \frac{0-3}{1-3} \cdot x_1 = 3 \cdot 249 = 747 \\
w_2 &= \lambda_2 \cdot x_2 = \frac{0-1}{2-1} \cdot \frac{0-3}{2-3} \cdot x_2 = -3 \cdot 292 = -876 \\
w_3 &= \lambda_3 \cdot x_3 = \frac{0-1}{3-1} \cdot \frac{0-2}{3-2} \cdot x_3 = 1 \cdot 369 = 369 \\
\end{aligned}\]
显然满足 \(w_1 + w_2 + w_3 = 747-876+369 = 240\) 。
为什么 \(w_1 + w_2 + w_3 = \lambda_1 \cdot x_1 + \lambda_2 \cdot x_2 + \lambda_3 \cdot x_3 = \lambda_1 \cdot f(1) + \lambda_2 \cdot f(2) + \lambda_3 \cdot f(3)\) 会恰好等于完整私钥 \(f(0)\) 呢?这是因为已知 3 个点的值 \(f(1)=249,f(2)=292,f(3)=369\) ,其拉格朗日插值多项式为:
\[L(x) = f(1) \cdot \frac{x-2}{1-2} \cdot \frac{x-3}{1-3} + f(2) \cdot \frac{x-1}{2-1} \cdot \frac{x-3}{2-3} + f(3) \cdot \frac{x-1}{3-1} \cdot \frac{x-2}{3-2} \]
而 \(f(0) = L(0) = \underbrace{f(1) \cdot \frac{0-2}{1-2} \cdot \frac{0-3}{1-3}}_{w_1} + \underbrace{f(2) \cdot \frac{0-1}{2-1} \cdot \frac{0-3}{2-3}}_{w_2} + \underbrace{f(3) \cdot \frac{0-1}{3-1} \cdot \frac{0-2}{3-2}}_{w_3}\)
8.2.1. 从多个 Shamir 分片恢复出完整私钥
在 \((t,n)\) 门限方案中,已知任意 \(t\) 个 Shamir 分片,都可以恢复出完整私钥。
其基本原理上节已经介绍过。以 \((3,n)\) 为例,完整私钥 \(f(0) = \lambda_1 \cdot f(1) + \lambda_2 \cdot f(2) + \lambda_3 \cdot f(3)\) ,其中 \(f(1),f(2),f(3)\) 就是 3 个 Shamir 分片。而 \(\lambda_1,\lambda_2,\lambda_3\) 不是秘密值,仅由参与者的下标就可以计算出来。
8.3. CVE-2023-33241
在节 4.1.1 中提到,GG18 协议没有严格地校验 Paillier 公钥 \(N_i\) 的合法性,这导致 GG18 出现了安全漏洞 CVE-2023-33241。
参考:
Practical Key-Extraction Attacks in Leading MPC Wallets 4.2 6ix1een Attack
Small Leaks, Billions Of Dollars: Practical Cryptographic Exploits That Undermine Leading Crypto Wallets
https://www.fireblocks.com/blog/gg18-and-gg20-paillier-key-vulnerability-technical-report/
8.3.1. 攻击原理
Alice Bob
在 Z_q 中随机生成 k_A
用 Alice 的公钥 N 加密 k_A,密文为 Enc(k_A)
-------------Enc(k_A)------------->
满足 β' < q^5 前提下随机选择 β'
在密文 Enc(k_A) 上用 Paillier 同态加密得到密文 c = Enc(k_A x_B + β')
记 β = -β'
<---------Enc(k_A x_B + β')--------
Alice 用私钥解密 Enc(k_A x_B + β'),其明文记为 α
如果把 MtA 子协议看作是黑盒子,则这个黑盒子的两个输入和两个输出分别是:
k_A # 输入。Alice 随机产生,只有 Alice 知道 x_B # 输入。Bob 的私钥分片,只有 Bob 知道 α # 输出。Alice 的输出,只有 Alice 知道 β # 输出。Bob 的输出,只有 Bob 知道
MtA 协议要很小心地处理,因为协议的输入输出都是敏感数据: \(k_A,\alpha\) 只能让 Alice 知道, \(x_B,\beta\) 只能让 Bob 知道。CVE-2023-33241 是针对 MtA 协议进行的攻击,让 Alice 获得了 Bob 的秘密 \(x_B\) 。
CVE-2023-33241 有两个关键点:
- 攻击关键点 1:MtA 协议中 Alice 使用更大的 \(k_A\) ,让 \(\beta'\) 不再起到 mask 的作用。也就是说 Alice 使用更大的 \(k_A\) 会导致 MtA 中 Bob 的秘密 \(x_B\) 被泄露(Alice 知道 \(x_B\) 后可以恢复出完整私钥)。
- 攻击关键点 2:Alice 伪造 \(k_A\) 的 Range Proof。MtA 协议中 Alice 需要提供 \(k_A < q^3\) 的 Range Proof。但在实施攻击关键点 1 后,由于 \(k_A\) 变大了,所以无法正常提供 Range Proof,需要伪造。
下面介绍一下第 1 个攻击关键点。为什么 MtA 协议中 Alice 使用更大的 \(k_A\) 时,会导致 Bob 的 \(x_B\) 被泄露。
首先看一下,Alice 让 \(k_A\) 取正常值(较小值)时,Bob 通过随机的 \(\beta'\) 可以使 Alice 无法猜测出 \(x_B\) : \[\begin{aligned} {\color{red}{k_A}} &= {\color{red}{\text{0x2381}}} \\ x_B &= \text{0x4193} \\ \beta'(\text{mask}) &= \text{0x4837813096} \\ {\color{red}{k_A}} \cdot x_B &= \text{0x9182413} \\ {\color{red}{k_A}} \cdot x_B + \beta' &= \text{0x48409954A9} \end{aligned}\]
而 如果 Alice 让 \(k_A\) 取较大值时,Bob 的 \(\beta'\) 将失去 mask 作用,导致 \(x_B\) 泄露(其实这里有个前提,即 \(\beta'\) 不能太大,如果 \(\beta'\) 比较大,那么 \(\beta'\) 将继续起到 mask 作用): \[\begin{aligned} {\color{red}{k_A}} &= {\color{red}{\text{0x100000000000}}} \\ x_B &= {\color{blue}{\text{0x4193}}} \\ \beta'(\text{mask}) &= \text{0x4837813096} \\ {\color{red}{k_A}} \cdot x_B &= {\color{blue}{\text{0x4193}}}\text{00000000000} \\ {\color{red}{k_A}} \cdot x_B + \beta' &= \underbrace{{\color{blue}{\text{0x4193}}}}_{泄露了 x_B}\text{0}\underbrace{\text{4837813096}}_{\beta' 失去 mask 作用} \end{aligned}\]
关于第 2 个攻击关键点,即就是 Alice 如何伪造 \(k_A\) 的 Range Proof(参见 GG18 Section A.1)的细节可参考节 8.3.2.1。
8.3.2. 攻击细节
下面以 \((2,n)\) 两方门限签名为例介绍一下攻击流程。假设两个参与者是 Alice 和 Bob,其中 Alice 为恶意攻击者。
- 在 DKG 阶段,Alice 按下面方式构造一个非法的 Paillier 公钥: \(N=p_1p_2 \cdots p_{16}z\) 。其中 \(p_1,p_2,\cdots,p_{16}\) 是 Alice 随机选择的大小为 \(2^{16}\) 的小素数(即这些素数都是 16 个比特位长);然后 Alice 随机选择一个大素数 \(z\) ,这个 \(z\) 不能太大,也不能太小,让 \(N\) 恰好可以满足对它的比特位长度要求即可( \(N\) 是 2048 个比特位长)。
- 假设 \(x_B\) 是 Bob 手头的私钥分片(即节 4.2.2.2 中的 Addtive Share \(w\) ),它是 256 比特位。Alice 和 Bob 每进行一次 MPC 签名,Alice 可以利用式子(后文会证明这个公式的正确性) \(x_B \bmod p_i = \frac{\alpha - (\alpha \bmod (N/p_i))}{N/p_i}\) 获得一个 \(x_B \bmod (N/p_i)\) ,其中 \(1\le i \le 16\) 。进行完 16 次签名后,Alice 就知道了 \[\begin{aligned} x_B & \bmod (N/p_1) \\ x_B & \bmod (N/p_2) \\ & \vdots \\ x_B & \bmod (N/p_{16}) \end{aligned}\] 然后利用中国剩余定理,可以计算出 \(x_B \bmod (p_1p_2\cdots p_{16})\) ,由于每个 \(p_i\) 都是 16 比特位,所以乘积 \(p_1p_2\cdots p_{16}\) 是 256 比特位,使用中国剩余定理可以计算出 256 比特位的 \(x_B\) 。
下面介绍一下 MPC 签名时,攻击者 Alice 获得值 \(x_B \bmod (N/p_i)\) 的细节。在 MPC 签名阶段,Alice 和 Bob 会利用 MtA 协议把积 \(k_A x_B\) 转换为两个数 \(\alpha\) 和 \(-\beta'\) 的和,也就是说 MtA 协议结束后有 \[k_Ax_B = \alpha + (- \beta')\] 其中 \(k_A\) 是 Alice 的秘密,而 \(x_B\) 是 Bob 的秘密(完整私钥的 Addtive Share), \(\alpha\) 是 MtA 结束后 Alice 获得的秘密值, \(-\beta'\) 是 MtA 结束后 Bob 获得的秘密值。
下面回顾一下 MtA 协议:
Alice Bob
在 Z_q 中随机生成 k_A
用 Alice 的公钥 N 加密 k_A,密文为 Enc(k_A)
-------------Enc(k_A)------------->
满足 β' < q^5 前提下随机选择 β'
在密文 Enc(k_A) 上用 Paillier 同态加密得到密文 c = Enc(k_A x_B + β')
<---------Enc(k_A x_B + β')--------
Alice 用私钥解密 Enc(k_A x_B + β'),其明文记为 α
MtA 结束后 Alice 得到 \(\alpha = (k_A x_B + \beta') \bmod N\) 。 恶意攻击者 Alice 在进行攻击时,并不在 \(Z_q\) 中随机产生 \(k_A\) ,而是使用一个更大值 \(k_A = \frac{N}{p_i}\) ,这样 MtA 结束后 Alice 得到 \(\alpha=(\frac{N}{p_i} x_B + \beta') \bmod N\) 。
注:在 GG18 中要求 Alice 提供一个零知识范围证明(参见 GG18 论文 A.1 Range Proof),Alice 需要证明她随机产生的 \(k_A\) 满足 \(k_A < q^3\) ,也就是 Alice 要证明 \(\frac{N}{p_i} < q^3\) 。由于 \(N\) 是 2048 比特位,而 \(p_i\) 是 16 比特位, \(q\) 为 256 比特位,所以 \(\frac{N}{p_i}\) 约为 2032 比特位,它肯定会大于 \(q^3\) 。也就是说正常情况下 Alice 无法提供这个零知识范围证明。 CVE-2023-33241 漏洞发现者利用 \(N\) (它也是 Range Proof 的参数)含有小因子 \(p_i\) 的特点,提出了一种特殊的构造 Range Proof 的方式(参考节 8.3.2.1),可以骗过 Bob 对 Range Proof 的校验,这是 CVE-2023-33241 能顺利实施的关键。
下面介绍一下为什么 \[x_B \bmod p_i = \frac{\alpha - (\alpha \bmod (N/p_i))}{N/p_i}\] 会成立。 推导过程中利用了一个重要前提 \(\beta' < q^5\) , 由于 \(q\) 是 256 比特位,显然 \(\beta'\) 的比特位不会超过 \(256 \times 5=1280\) 位,又由于 \(N\) 的比特位为 2048, \(p_i\) 的比特位为 16,所以一定有 \[\beta' < \frac{N}{p_i}\]
因为 \(\alpha = x_B \frac{N}{p_i} + \beta' \bmod N\) ,且 \(\frac{N}{p_i}\) 是 \(N\) 的因子,利用同余性质 \(a \equiv b{\pmod {cn}} \Rightarrow a \equiv b{\pmod {n}}\) ,所以 \(\alpha \bmod \frac{N}{p_i} = ( x_B \frac{N}{p_i} + \beta' ) \bmod \frac{N}{p_i} = 0 + \beta' \bmod \frac{N}{p_i}\) ,即有 \[\begin{aligned} \alpha \bmod \frac{N}{p_i} & = \underbrace{\beta'}_{< N/p_i} \bmod \frac{N}{p_i} \\ & = \beta' \end{aligned}\]
下面开始推导 \(x_B \bmod p_i = \frac{\alpha - (\alpha \bmod (N/p_i))}{N/p_i}\) ,从式子右边的分子开始推导 \[\begin{aligned} \alpha - (\alpha \bmod \frac{N}{p_i}) &= \alpha - \beta' \\ &= ((x_B \frac{N}{p_i} + \beta') \bmod N ) - \beta' \\ &= (x_B \frac{N}{p_i} \bmod N ) + (\beta' \bmod N) - \beta' \\ &= (x_B \frac{N}{p_i} \bmod N) + \beta' - \beta' \\ &=x_B \frac{N}{p_i} \bmod N \\ & \stackrel{?}{=} \frac{N}{p_i} (x_B \bmod p_i) \end{aligned}\] 所以有 \(x_B \bmod p_i = \frac{\alpha - (\alpha \bmod (N/p_i))}{N/p_i}\) 。不过上面推导中最后一步 \(x_B \frac{N}{p_i} \bmod N=\frac{N}{p_i} (x_B \bmod p_i)\) 为什么会成立呢?下面将证明这个等式。因为 \[x_B = \lfloor \frac{x_B}{p_i} \rfloor p_i + (x_B \bmod p_i)\] 对上式两边乘以 \(N/p_i\) ,有 \[x_B \frac{N}{p_i} = \lfloor \frac{x_B}{p_i} \rfloor p_i \frac{N}{p_i} +(x_B \bmod p_i) \frac{N}{p_i}\] 对上式两边取 \(\bmod N\) ,有 \[\begin{aligned} x_B \frac{N}{p_i} \bmod N &= 0 + \left( \underbrace{ \underbrace{(x_B \bmod p_i)}_{< p_i} \frac{N}{p_i}}_{< N} \bmod N \right) \\ &= (x_B \bmod p_i) \frac{N}{p_i} \end{aligned}\]
注:GG18 论文有两个版本(初始版本和 2021 年的修订版本,如表 1 所示),前面提到了攻击依赖于 \(\beta' < q^5\) ,这个前提只存在于 2021 的修订版本中,节 8.3.1 中也提到了当 \(\beta'\) 较大时,攻击是不能成功的。
| GG18 版本 | 论文中要求 \(\beta'\) 范围 | 攻击 |
|---|---|---|
| 初始版本 | \(< N\) | 通过 16 次签名可计算出 \(x_B\) ,从而恢复出完整私钥 |
| 2021 年修订版本 | \(< q^5\) | Death by 1M Cuts. 经过 1 百万次签名尝试可能盗走 \(x_B\) |
8.3.2.1. 伪造 Range Proof
GG18 中的 Range Proof 如图 6 所示。

Figure 6: GG18 Range Proof
当 Alice 使用 Range Proof 证明她的 \(k_A\) 在范围 \([-q^3, q^3]\) 中时,上面的记号 \(m\) 就是 Alice 的 \(k_A\) , \(c\) 是 \(m\) 的 Paillier 密文,即 \(c=\text{Enc}(m)=\Gamma^m r^N \bmod N^2 = (1+N)^m r^N \bmod N^2\) (在 Paillier 公钥中 \(\Gamma=1+N\) 是一个常用设定)。Alice 需要证明 Paillier 密文 \(c\) 的对应明文 \(k_A\) 在范围 \([-q^3, q^3]\) 中。
Bob 会校验下面式子是否成立: \[\begin{aligned} s_1 & \le q^3 \\ u c^e &= \Gamma^{s_1} s^N \bmod N^2 \\ h_1^{s_1} h_2^{s_2} z^{-e} &= w \bmod \tilde{N} \end{aligned}\] 如果都成立,则 Bob 相信 Alice 发送给他的 Paillier 密文 \(c\) 对应的明文 \(m\) 会满足 \(m \in [-q^3, q^3]\) 。
Alice 发送给 Bob 的 \(s_1\) 是这样计算的 \(s_1 = em + \alpha = \text{Hash}(N,\Gamma,c,z,u,w) m + \alpha\) (图 6 是交互式的协议,通过 Fiat–Shamir heuristic 可转移为非交互式的协议,把 \(e\) 用 \(\text{Hash}(N,\Gamma,c,z,u,w)\) 替换即可),由于 \(m=k_A=\frac{N}{p_i}\) ,它有 2032 个比特位,显然 Bob 在校验 \(s_1 \le q^3\) 是否成立时,会发现这个不等式不成立。那怎么办呢?Alice 采用的办法是 令 \(m=0\) 来生成 Range Proof,这样 \(s_1 \le q^3\) 就一定成立了。
这带来了一个新问题。因为 Alice 发送给 Bob 的 \(c\) 是 \(m=\frac{N}{p_i}\) 的密文(并不是 \(m=0\) 的密文),这将导致 Bob 的第 2 个校验 \(u \cdot \text{Enc}(\frac{N}{p_i})^e = \Gamma^{s_1} s^N \bmod N^2\) 不成立。Alice 的办法是通过 修改由 Alice 产生的随机数(如 Range Proof 中的 \(\alpha,\beta,\gamma,\rho\) )的值来操作 \(e\) 直到 \(\text{Enc}(\frac{N}{p_i})^e = \text{Enc}(0)^e \bmod N^2\) 成立。 因为 \(\text{Enc}(\frac{N}{p_i})^e = \text{Enc}(0)^e \bmod N^2\) 成立的话,Bob 的校验 \(u \cdot \text{Enc}(\frac{N}{p_i})^e = \Gamma^{s_1} s^N \bmod N^2\) 就肯定成立了。因为这个式子的 \(s_1\) 就是按 \(m=0\) 计算来的,显然有 \(u \cdot \text{Enc}(0)^e = \Gamma^{s_1} s^N \bmod N^2\) 成立,又因为 \(\text{Enc}(\frac{N}{p_i})^e = \text{Enc}(0)^e \bmod N^2\) ,所以 \(u \cdot \text{Enc}(\frac{N}{p_i})^e = \Gamma^{s_1} s^N \bmod N^2\) 成立。现在剩下的问题是 \(e\) 满足什么条件时 \(\text{Enc}(\frac{N}{p_i})^e = \text{Enc}(0)^e \bmod N^2\) 会成立?答案是 \(e \bmod p_i = 0\) ,也就是说 Alice 修改由她产生的随机数(如 \(\alpha,\beta,\gamma,\rho\) ,这会导致 \(e=\text{Hash}(N,\Gamma,c,z,u,w)\) 发生变化,直到 \(e\) 是 \(p_i\) 的倍数(由于 \(p_i\) 只有 16 个比特位,所以找到这样的 \(e\) 并不困难)。 记 \(e=a p_i\) (其中 \(a\) 是整数),证明如下: \[\begin{aligned} \text{Enc}(\frac{N}{p_i})^e \bmod N^2 &= \left( (1+N)^{\frac{N}{p_i}} r^N \bmod N^2\right)^e \bmod N^2 \\ &= (1+N)^{\frac{N}{p_i}e} r^{Ne} \bmod N^2 \\ &= (1+N)^{\frac{N}{p_i} a p_i} r^{Ne} \bmod N^2 \\ &= (1+N)^{Na} r^{Ne} \bmod N^2 \\ &= ((1+N)^{Na} \bmod N^2)( r^{Ne} \bmod N^2 ) \bmod N^2 \\ &= ((1+NNa) \bmod N^2) ( r^{N} \bmod N^2 )^e \bmod N^2 \\ &= 1 \cdot ( r^{N} \bmod N^2 )^e \bmod N^2 \\ &= \text{Enc}(0)^e \bmod N^2\end{aligned}\]
上面推导中用到了结论 \((1+N)^x = (1 + nx) \bmod N^2\) ,参考:https://en.wikipedia.org/wiki/Paillier_cryptosystem#Background
8.3.3. 修复方案
根据攻击原理,我们可以得到下面的修复方案:
- 参与者公布 Paillier 公钥 \(N_i\) 给其它参与者时,需要证明 \(N_i\) 是合法的 Paillier 公钥,也就是说 \(N_i\) 确实是两个安全素数 \(p_i,q_i\) 的乘积,且这两个安全素数确实满足 Paillier 私钥的要求(即 \(p_iq_i\) 和 \((p_i-1)(q_i-1)\) 互素),关于这个零知识证明协议可以参考 UC Non-Interactive, Proactive, Threshold ECDSA (CMP) 的 4.3 节 Paillier-Blum Modulus ZK。
- 使用零知识证明协议证明 \(N_i\) 没有小因子,即 \(p_i,q_i\) 都是比较大的素数,关于这个零知识证明协议可以参考 UC Non-Interactive, Proactive, Threshold ECDSA (CMP) 的 B.4 节 No Small Factor Proof。
节 4.1.1 中也提到了这些修复方案。
9. 参考
Fast Multiparty Threshold ECDSA with Fast Trustless Setup
A Threshold Cryptosystem without a Trusted Party
Secure Distributed Key Generation for Discrete-Log Based Cryptosystems
Distributed Key Generation and Its Applications, by Aniket Pundlik Kate
A Survey of ECDSA Threshold Signing
https://www.youtube.com/watch?v=PdfDZIwuZm0
https://www.youtube.com/watch?v=wtxH3PuMAgQ
https://www.fireblocks.com/blog/gg18-and-gg20-paillier-key-vulnerability-technical-report/
