Schnorr Threshold Signature (FROST)
Table of Contents
1. 论文介绍
2020 年,Chelsea Komlo 和 Ian Goldberg 在论文 FROST: Flexible Round-Optimized Schnorr Threshold Signatures 中提出了一种 Schnorr 门限签名方案,简称为 FROST 协议,本文将介绍它。
1.1. 本文记号
门限方案 \((t,n)\) 表示至少需要 \(t\) 个参与者合作才能完成签名。注:记号 \((t,n)\) 在其它论文中含义可能不同,有的表示至少需要 \(t+1\) 个参与者合作才能完成签名。
2. 基础知识
2.1. Schnorr 签名
在介绍 Schnorr 门限签名之前,先介绍一下常规的 Schnorr 签名。
假设私钥为 \(s \in \mathbb{Z}_q\) ,而公钥为 \(Y = g^s \in \mathbb{G}\) ,待签名消息为 \(m\) ,Schnorr 签名过程如下:
- 随机选择 \(k \leftarrow \mathbb{Z}_q\) ,计算 \(k\) 的 commitment \(R = g^k \in \mathbb{G}\) ;
- 计算 Challenge \(c = H(R,Y,m)\) ;
- 使用私钥 \(s\) 计算 \(z = k + s \cdot c \in \mathbb{Z}_q\) ;
- 对 \(m\) 的签名数据就是 \(\sigma=(R, z)\) 。
验证签名过程(输入数据有 \(R,z,m,Y\) )如下:
- 推导出 Challenge \(c = H(R,Y,m)\) ;
- 计算 \(R' = g^z \cdot Y^{-c}\) ;
- 如果 \(R \stackrel{?}{=} R'\) 成立,则说明签名合法。
注:你会在一些资料中会看到采用 \(c = H(R,m)\) 的方式来计算 Challenge;但在 BIP340 中采用 \(c = H(R,Y,m)\) 来计算 Challenge,也就是让公钥 \(Y\) 参与了 Challenge 的计算,这主要是为了避免 “related key attacks” (e.g. attacks with BIP32 unhardened derived keys),参考:https://bitcoin.stackexchange.com/questions/115315/to-what-extent-does-bip32-key-derivation-impact-the-design-of-secure-key-aggrega
3. FROST 协议介绍
3.1. FROST Keygen 协议
FROST 中的 Keygen 协议是 Pedersen's DKG 的一种变种:在 Pedersen's DKG 的基础上引入了对秘密值的零知识证明来防止 Rogue Key Attack(注:Rogue Key Attack 在论文 Randomness Re-use in Multi-recipient Encryption Schemeas 有介绍)。
本文不详细介绍 FROST 中的 Keygen 协议,只给出结论。
3.1.1. 私钥分片
对于门限方案 \((t,n)\) ,当 Keygen 协议结束后,每个参与者 \(P_i, i=\{1,2,\cdots,n\}\) 会得到:
- \(P_i\) 的私钥分片 \(s_i = F(i)\) ,而完整的私钥 \(s = F(0)\) ,其中 \(F(x)\) 是某个 \(t-1\) 次多项式。也就是说 \(n\) 个私钥分片就是 \(t-1\) 次曲线上的 \(n\) 个点 \((1, s_1), (2, s_2), \cdots, (n, s_n)\) 。
- 所有参与者私钥分片 \(s_j, j=\{1,2,\cdots,n\}\) 所对应的 commitment \(Y_j = g^{s_j}\) 。
下面介绍一下完整私钥 \(s\) 和私钥分片 \(s_i\) 的关系。假设 \(\alpha\) 是参与签名的参与者数量,满足 \(t \le \alpha \le n\) ,这 \(\alpha\) 个参与者所拥有的私钥分片对应的 \(x\) 轴坐标的集合为 \(S=\{p_1, \cdots, p_{\alpha}\}\) ,设 \(\lambda_i\) 为拉格朗日系数,即: \[\lambda_i = \prod_{j=1,j \ne i}^{\alpha} \frac{p_j}{p_j - p_i}\] 根据拉格朗日插值相关知识可知 \(s\) 和 \(s_i\) 满足关系: \[s = \sum_{i\in S} \lambda_i \cdot s_i\]
下面通过实例来验证一下上面的结论。假设门限方案 \((t,n) = (3,5)\) ,也就是说共有 \(5\) 个参与者,至少需要 \(3\) 个参与者合作才能完成签名。Keygen 时的 \(t-1\) 次多项式为 \(F(x)=2x^{2} - 5x + 4\) ,Keygen 结束后得到的 \(5\) 个私钥分片分别为 \((1, 1),(2, 2),(3, 7),(4, 16),(5, 29)\) ,完整的私钥 \(s=F(0)=4\) ,假设某次签名时,选择了其中 \(4\) 个参与者 \(P_1, P_2, P_3, P_5\) ,这个例子中 \(S=\{1,2,3,5\}\) ,下面来验证一下 \[s \stackrel{?}{=} \lambda_1 s_1 + \lambda_2 s_2 + \lambda_3 s_3 + \lambda_5 s_5\] 是否成立。
由于 \[\begin{aligned}
\lambda_1 \cdot s_1 &= \frac{2}{2-1} \cdot \frac{3}{3-1} \cdot \frac{5}{5-1} \cdot s_1 = \frac{15}{4} \cdot s_1 = \frac{15}{4} \\
\lambda_2 \cdot s_2 &= \frac{1}{1-2} \cdot \frac{3}{3-2} \cdot \frac{5}{5-2} \cdot s_2 = -5 \cdot s_2 = -10 \\
\lambda_3 \cdot s_3 &= \frac{1}{1-3} \cdot \frac{2}{2-3} \cdot \frac{5}{5-3} \cdot s_3 = \frac{5}{2} \cdot s_3 = \frac{35}{2} \\
\lambda_5 \cdot s_5 &= \frac{1}{1-5} \cdot \frac{2}{2-5} \cdot \frac{3}{3-5} \cdot s_5 = -\frac{1}{4} \cdot s_5 = -\frac{29}{4} \\
\end{aligned}\] 从而可知 \(\lambda_1 s_1 + \lambda_2 s_2 + \lambda_3 s_3 + \lambda_5 s_5 = 4\) ,显然它就是完整私钥 \(s\) 。
3.2. FROST 签名协议
FROST 签名协议是一个 Two Rounds 协议。由于第一轮操作不会涉及到待签名消息 \(m\) ,所以它可以提前进行,这一轮就是论文中所说的“预处理阶段”。
FROST 协议中有个 Signature Aggregator 角色,在具体实现时可以去掉这个角色,具体方法是每个签名参与者都充当这个角色,这样以前发送给 Signature Aggregator 的消息就改为发送给所有其它签名参与者。注:如果存在 Signature Aggregator 角色,各个签名参与者只需要和 Signature Aggregator 之间发送消息,并不需要和其它签名参与者相互发送消息,这点从图 1 和图 2 中可知。
注:很多 Two Rounds 协议都不能抵抗 Wagner/Drijvers Attack ,FROST 协议可以抵抗 Wagner/Drijvers Attack,这里不详细介绍细节,可参考 FROST 原论文第 5.2 节。
3.2.1. Round One
FROST 签名第一轮操作:每个签名参与者随机选择 \(d_i, e_i\) (需要暂存起来,第二轮操作时需要用到),计算出 \(D_i = g^{d_i}, E_i=g^{e_i}\) ,然后把 \(D_i, E_i\) 发送给 Signature Aggregator。
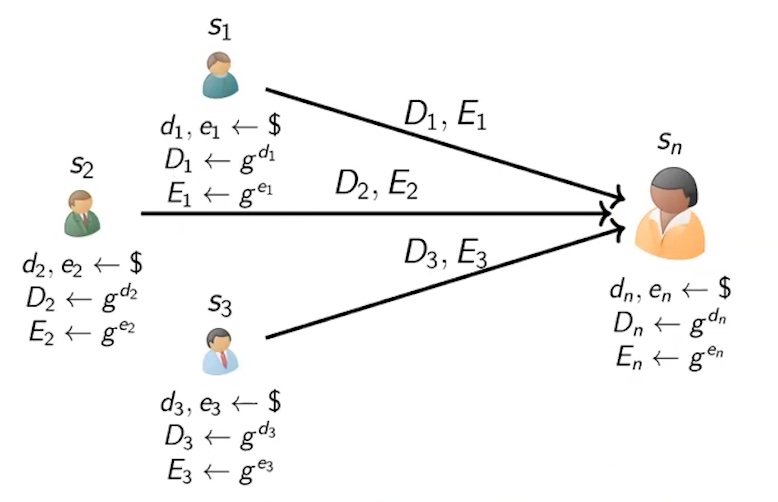
Figure 1: FROST 签名第一轮操作,右边是 Signature Aggregator。摘自:https://www.youtube.com/watch?v=tKR4QKhmXXI
3.2.2. Round Two
先介绍几个记号定义 \[\begin{aligned} k &= \sum_{i \in S} k_i \\ k_i &= d_i + e_i \cdot \rho_i \\ R_i &= g^{k_i} = g^{d_i + e_i \cdot \rho_i} = D_i \cdot (E_i)^{\rho_i} \end{aligned}\]
FROST 签名第二轮操作:Signature Aggregator 选择 \(\alpha (t \le \alpha \le n)\) 个参与者,记这个 \(\alpha\) 个参与者所拥有的私钥分片对应的 \(x\) 轴坐标的集合为 \(S\) ,Signature Aggregator 把收集来的 \(D_i, E_i\) 组成一个列表 \(B = \left<(i, D_i, E_i)\right>_{i \in S}\) ,然后和待签名消息 \(m\) 一起发送给这 \(\alpha (t \le \alpha \le n)\) 个参与者;签名参与者收到 \((m,B)\) 后,按图 2 中的方式计算出 \(z_i\) 后,把 \(z_i\) 发送给 Signature Aggregator;Signature Aggregator 收到 \(z_i\) 后,验证每个 \(z_i\) 对于 \(g^{z_i} \stackrel{?}{=} R_i \cdot Y_i^{\lambda_i \cdot c}\) 成立是否(为什么它会成立呢?这是因为 \(z_i\) 可以看作是把 \(\lambda_i \cdot s_i\) 当作完整私钥所对应的签名数据,这时完整公钥是 \(g^{\lambda_i \cdot s_i} = Y_i^{\lambda_i}\) ,验证 \(g^{z_i} \stackrel{?}{=} R_i \cdot Y_i^{\lambda_i \cdot c}\) 其实就是验证一个常规的 Schnorr 签名),如果成立,则把 \(z = \sum z_i\) 作为最终的签名数据 \(z\) 。而签名数据的另一部分 \(R = \prod_{i \in S} D_i \cdot (E_i)^{\rho_i}\) ,其中 \(D_i,E_i\) 是公开数据,而 \(\rho_i\) 也可以利用公开数据算出来的,所以 \(R\) 容易算出来。

Figure 2: FROST 签名第二轮操作。摘自:https://www.youtube.com/watch?v=ReN0kMzDFro
3.2.3. FROST 签名的正确性
为什么 FROST 协议会产生和常规的 Schnorr 签名(参见节 2.1)相同的签名数据呢?Schnorr 签名数据分为 \(R,z\) 两部分,下面分别讨论 \(R,z\) 的正确性。
下面讨论 \(R\) 的正确性:
\[\begin{aligned} R &= g^k & \text{(这是常规 Schnorr 计算 R 的方式)}\\
&= g^{\sum_{i \in S} k_i} \\
&= g^{\sum_{i \in S} (d_i + e_i \cdot \rho_i)} \\
&= \prod_{i \in S} R_i \\
&= \prod_{i \in S} D_i \cdot (E_i)^{\rho_i} & \text{(这是 FROST Schnorr 计算 R 的方式)}\\
\end{aligned}\]
下面讨论 \(z\) 的正确性:
\[\begin{aligned} z &= k + s \cdot c & \text{(这是常规 Schnorr 计算 z 的方式)}\\
&= \sum_{i \in S} k_i + s \cdot c \\
&= \sum_{i \in S} (d_i + e_i \cdot \rho_i) + s \cdot c & \text{(假设 s = Σ λᵢ sᵢ)}\\
&= \sum_{i \in S} (d_i + e_i \cdot \rho_i) + \sum_{i\in S} \lambda_i \cdot s_i \cdot c \\
&= \sum_{i \in S} (d_i + e_i \cdot \rho_i + \lambda_i \cdot s_i \cdot c) \\
&= \sum_{i \in S} z_i & \text{(这是 FROST Schnorr 计算 z 的方式)}\\
\end{aligned}\]
在上面推导中用到了等式 \(s = \sum_{i\in S} \lambda_i \cdot s_i\) ,它是否成立呢?答案是肯定的,参考节 3.1.1 。至此,我们已经证明了 FROST 协议产生的签名数据和常规的 Schnorr 签名一样。
4. 和其它方案的对比
4.1. 对比指标:Robust 和 Non-Robust
Robust 签名方案是指,只要参与者中有 \(t\) 个参与者是诚实的(即它们遵守协议),那么就一定可以得到正确的签名,就算其中有恶意参与者也无所谓。 比如,在 \((3,5)\) 方案中,现在有 \(4\) 个参与者参与签名,其中诚实参与者是 \(3\) 个,而恶意参与者是 \(1\) 个,在 Robust 签名方案下可以得到正确的签名。
Non-Robust 签名方案是指,发现有恶意参与者(即它们不遵守协议)就退出协议,从而这一次没有办法得到正确的签名,需要把恶意参与者踢除后重新运行签名。
显然,Robust 方案要优于 Non-Robust 方案。不过,本文介绍的 FROST 及 GG18(一个著名的 ECDSA 门限签名方案)都只是 Non-Robust 方案。
4.2. 和 Stinson and Strobl 方案的对比
2001 年,D.R. Stinson and R.Strobl 在论文 Provably Secure Distributed Schnorr Signatures and a (t,n) Threshold Scheme for Implicit Certificates 中提出了一种 Schnorr 门限签名,下面称为 Stinson and Strobl 方案。这个方案是一种 Robust 签名方案,不过它签名所需要的轮次(为 4)比 FROST 方案的轮次(为 2)要多。
Stinson and Strobl 方案和 FROST 方案的对比如表 1 所示。
| Rounds of Signing | Robust | |
|---|---|---|
| Stinson and Strobl 方案 | 4 | Yes (Better) |
| FROST | 2 (Better) | No |
注:虽然 FROST 不是 Robust 协议(也就是说存在恶意参与者时协议会失败),但 FROST 可以检测出恶意参与者,这样在发现恶意参与者时可以把它踢除后重新运行签名即可,所以这也不是什么大问题。
5. 兼容 BIP340
Bitcoin 的 Taproot 地址采用了 Schnorr 签名,BIP340 中规定了相关细节。
为了让公钥及签名(Schnorr 签名中有一部分数据就是公钥)更短,BIP340 中编码曲线上的点(如公钥)时,只使用了点的 X 坐标,省略了点的 Y 坐标。根据椭圆曲线逆元素的定义,设点 \(P=(x,y)\) ,则其逆元素 \(-P = (x, -y \bmod p)\) ,一个点只编码 X 坐标时,点 \(P\) 和 \(-P\) 是不可区分的。
只使用 X 坐标编码一个点显然会导致一个问题: 每个公钥会对应两个私钥 \(s\) 和 \(-s\) ,为了消除歧义,在进行 Schnorr 签名时,BIP340 规定了公钥 Y 坐标为偶数的那个私钥参与签名,且规定一次一用的 \(k\) 对应的公钥其 Y 坐标也必须是偶数。
这里有个隐含的事实:对于椭圆曲线上的两个点 \(P=(x,y)\) 和 \(-P = (x, -y \bmod p)\) ,其中一定有个点的 Y 坐标是奇数,而另一个点的 Y 坐标是偶数,证明如下:
- 假设 P 的 Y 坐标为奇数,即 \(y\) 是奇数。由于椭圆曲线 secp256k1 的 \(p\) 是奇数, \(-y \bmod p=(p - y) \bmod p = p - y\) ,奇数减去奇数一定是偶数,所以 \(-P\) 的 Y 坐标是偶数;
- 假设 P 的 Y 坐标为偶数,即 \(y\) 是偶数。由于椭圆曲线 secp256k1 的 \(p\) 是奇数, \(-y \bmod p=(p - y) \bmod p = p - y\) ,奇数减去偶数一定是奇数,所以 \(-P\) 的 Y 坐标是奇数。
FROST 兼容 BIP340 要做的事项:
- Keygen 时,如果发现完整私钥 \(s = \sum_{i\in S} \lambda_i \cdot s_i\) 对应公钥 \(P\) 的 Y 坐标为奇数,则每个参与者把自己的私钥分片 \(s_i\) 取反,这会使得新的完整私钥 \(s' = - \sum_{i\in S} \lambda_i \cdot s_i = -s\) 对应公钥的 Y 坐标为偶数,满足 BIP340 要求;
- FROST 签名时,如果在 Round Two 中发现 \(k = \sum_{i \in S} k_i\) 对应公钥 \(R\) 的 Y 坐标为奇数,则每个参与者都把自己的 \(d_i,e_i\) 取反,这会新的 \(k' = - \sum_{i \in S} k_i = -k\) 对应公钥的 Y 坐标为偶数,满足 BIP340 要求;
- FROST 签名时,Challenge \(c\) 的计算改为 BIP340 所要求的 \(hash_{BIP0340/challenge}(bytes(R) || bytes(P) || m)\) 。
参考:https://github.com/jesseposner/FROST-BIP340/blob/2c0d86e6e692341b0477968d61d85b8654d5d9c3/frost.py
6. 参考
本文主要参考下面资料:
- FROST: Flexible Round-Optimized Schnorr Threshold Signatures
- FROST: Flexible Round-Optimized Schnorr Threshold Signatures, YouTube, Speaker: Ian Goldberg
- FROST: Flexible Round-Optimized Schnorr Threshold Signatures, YouTube, Speaker: Chelsea Komlo
- FROST Rust 实现:https://github.com/ZcashFoundation/frost