Shamir's Secret Sharing and Verifiable Secret Sharing (VSS)

1. 背景介绍
2. Shamir's Secret Sharing 方案
- 2.1. Shamir's Secret Sharing 实例
- 2.2. 系数在有限域中的多项式运算
3. Verifiable Secret Sharing（VSS）
- 3.1. Feldman's Verifiable Secret Sharing
- 3.2. Pedersen's Verifiable Secret Sharing
4. Publicly Verifiable Secret Sharing（PVSS）
5. Asynchronous Verifiable Secret Sharing（AVSS）
6. Distributed Key Generation（DKG）
7. 参考

1. 背景介绍

问题描述：有一个秘密值 \(d\) ，需要拆分为 \(n\) 个部分，分别交给 \(n\) 个成员保管，当有 \(t\; (t \le n)\) 个成员提供他们保管的信息后就能恢复出秘密值 \(d\) ，如果小于 \(t\) 个成员提供信息则不能恢复。

Adi Shamir（2002 年图灵奖获得者）于 1979 年在论文 How to share a secret 中提出的一种共享秘密的方案。

2. Shamir's Secret Sharing 方案

Shamir 方案的秘密分发过程为：随机取 \(t-1\) 个数 \(a_1, a_2, \cdots, a_{t-1}\) ，构造下面多项式： \[f(x) = d + a_1 x + a_2 x^2 + \cdots + a_{t-1}x^{t-1}\] 其中 \(d\) 是秘密值，然后令 \(x=1,2,\cdots,n\) 这样得到的 \(f(x)\) 分别记为部分秘密 \(d_i\) 由一个可信赖的第三方（一般称为 Dealer）分配给 \(n\) 个成员，也就是 \(d_i = f(i)\) 其中 \(i=1,2\cdots, n\) 。

秘密值 \(d\) 由 \(t\) 个部分秘密重建的步骤为： \(t\) 个成员拿出他们的部分秘密 \(d_i\) ，我们可以把点 \((1, d_1), (2, d_2), \cdots, (t, d_t)\) 重建为一个唯一的 \(t-1\) 次多项式，记为 \(h(x)\) ，由拉格朗日插值公式有 \[h(x) = \sum_{i=1}^{t}d_i \lambda_{i}(x)\] 其中 \(\lambda_{i}(x) = \prod\limits_{k \in S \setminus i} \frac{x-k}{i-k}\) ，这里 \(S\) 是 \(t\) 个点的 \(x\) 坐标组成的集合，则秘密值 \(d=h(0)\)

显然，Shamir's Secret Sharing 能正确工作的核心在于： 2 个点可以唯一确定一个 1 次多项式（直线），3 个点可以唯一确定一个 2 次多项式（抛物线），依此类推， \(t\) 个点可以唯一地确定一个 \(t-1\) 次多项式。这样，上面过程中的 \(h(x)\) 就是 \(f(x)\) ，从而 \(d=h(0)\) 就是 \(f(0)\) 。

图 1（改编自 https://arxiv.org/pdf/1302.1185.pdf ）是 Shamir's Secret Sharing 方案的示意图。

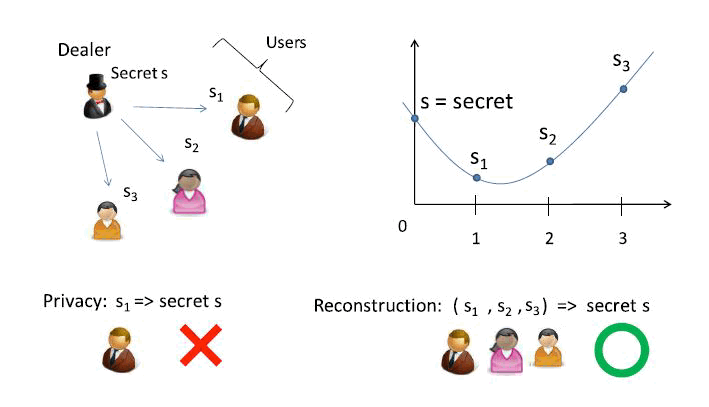
Figure 1: Shamir's Secret Sharing 示意图

Shamir 方案中， \(n\) 个成员相当于从 \(t-1\) 次多项式对应曲线上取了 \(n\) 个点，而恢复 \(t-1\) 次多项式仅仅需要 \(t\) 个点就够了，这样就实现了任意 \(t\) 个成员都可恢复出同一个 \(t-1\) 次多项式，我们事先把秘密值 \(d\) 编码到多项式中（具体做法就是 \(x\) 取 0 时的 \(y\) 值作为秘密值），就可以恢复秘密值了。注：在实践中，我们往往在有限域上进行运算，这样可以避免浮点数进行计算时的精度误差。

参考：https://en.wikipedia.org/wiki/Shamir%27s_Secret_Sharing

2.1. Shamir's Secret Sharing 实例

假设秘密值 \(d = 1234\) ，要把这个秘密值分发给 \(n=6\) 个成员，任意 \(t=3\) 个成员可以重新恢复秘密值。具体的操作过程如下。

首先，随机取 \(t-1=2\) 个值，假设这两个随机值为 166 和 94，则构造出下面多项式 \[f(x)=1234 + 166 x + 94x^2\]

然后，在这个多项式对应曲线上计算 6 个点 \[D_1 = (1, 1494), D_2 = (2, 1942), D_3 = (3, 2578), D_4 = (4, 3402), D_5 = (5, 4414), D_6 = (6, 5614)\] 把这 6 个信息分配给 6 个成员。

现在假设 3 个成员 \(D_2,D_4,D_5\) 想恢复出秘密值，怎么操作呢？

记： \((x_1,y_1)=(2, 1942),(x_2,y_2)=(4, 3402),(x_3,y_3)=(5, 4414)\) ，计算拉格朗日系数：

\begin{aligned}\lambda_{x_1}(x) &= \frac{x-x_2}{x_1 - x_2} \cdot \frac{x-x_3}{x_1 - x_3} = \frac{x-4}{2-4} \cdot \frac{x-5}{2-5} = \frac{1}{6}x^2 - \frac{3}{2} x + \frac{10}{3} \\ \lambda_{x_2}(x) &= \frac{x-x_1}{x_2 - x_1} \cdot \frac{x-x_3}{x_2 - x_3} = \frac{x-4}{4-2} \cdot \frac{x-5}{4-5} = -\frac{1}{2}x^2 + \frac{7}{2} x - 5 \\ \lambda_{x_3}(x) &= \frac{x-x_1}{x_3 - x_1} \cdot \frac{x-x_2}{x_3 - x_2} = \frac{x-2}{5-2} \cdot \frac{x-4}{5-4} = \frac{1}{3}x^2 - 2 x + \frac{8}{3} \\ \end{aligned}

由拉格朗日插值公式有 \[\begin{aligned} f(x) &= \sum_{j=1}^3 y_j \cdot \lambda_{x_j}(x) \\ &= y_1 \lambda_{x_1}(x) + y_2 \lambda_{x_2}(x) + y_3 \lambda_{x_3}(x) \\ &= 1942 (\frac{1}{6}x^2 - \frac{3}{2} x + \frac{10}{3}) + 3402( -\frac{1}{2}x^2 + \frac{7}{2} x - 5) + 4414 ( \frac{1}{3}x^2 - 2 x + \frac{8}{3} ) \\ &= 1234 + 166x + 94 x^2 \end{aligned}\]

从而秘密值 \(d = f(0) = 1234\)

2.2. 系数在有限域中的多项式运算

在 2.1 中介绍的例子使用的是普通整数系数的多项式运算，这只能用于原理性演示，不能直接用于真实环境，因为它是不安全的。系数是普通整数这个约束，会让秘密值 \(d\) 的可能范围大大缩小。比如，在 2.1 中的例子中，如果某人已知两个点 \(D_1 = (1, 1494), D_2 = (2, 1942)\) ，尽管他不能直接计算出秘密值 \(d\) ，但可以推测出 \(d\) 的可能范围 \(d \in [1046, 1048, \cdots, 1342, 1344]\) ，这里不详细介绍，详情可参考：https://en.wikipedia.org/wiki/Shamir%27s_secret_sharing#Problem_of_using_integer_arithmetic

为了解决这个问题，可以使用系数在有限域中的多项式运算，有兴趣的读者可参考：密码编码学与网络安全——原理与实践（第七版），5.5 节多项式运算。

3. Verifiable Secret Sharing（VSS）

Shamir's Secret Sharing 方案中，有个假设：Dealer（即编码秘密值，分配部分秘密给各个参与者的人）是可信的。如果 Dealer 做恶，比如分配给各个参与者的部分秘密是不一致的随便的值，那么造成的结果是灾难性的：可能某 3 个人恢复出来的完整秘密值是 \(d_1\) ，而另外 3 个人恢复出来的完整秘密值是另一个值 \(d_2\) 。

Verifiable Secret Sharing（VSS）可以解决这个问题，它能检测出做恶的 Dealer。

3.1. Feldman's Verifiable Secret Sharing

下面介绍 1987 年 Feldman 在论文 A Practical Scheme for Non-interactive Verifiable Secret Sharing 中提出的 VSS 方案（ \(g\) 是循环群 \(G\) 的生成元）：

Dealer 随机选择多项式 \[p(x) = s + a_1 x + a_2 x^2 + \cdots + a_t x^t\] 这里， \(s\) 是秘密值，把 \(p(1), p(2), \cdots, p(n)\) 通过加密通道分配给参与者 \(P_i, 1 \le i \le n\) ，任意 \(t+1\) 个参与者可以恢复出 \(s\) ，少于或者等于 \(t\) 个参与者无法恢复出 \(s\) 。
Dealer 同时公开下面信息： \[\begin{aligned} c_0 &= g^s \\ c_1 &= g^{a_1} \\ \cdots \\ c_t &= g^{a_t}\end{aligned}\] 由这些公开的信息是不能反推出多项式系数的（本文表述中的模运算全部省略了）。
每个参与者 \(P_i\) 验证自己收到的 \(p(i)\) ，如果 \[g^{p(i)} = c_0 c_1^i c_2^{i^2} \cdots c_t^{i^t}\] 成立（注：把 \(g^{p(i)}\) 中的 \(p(i)\) 按定义展开就可推导出右边），则通过验证，如果不成立就终止协议。

3.2. Pedersen's Verifiable Secret Sharing

下面介绍 1991 年 Pedersen 在论文 Non-Interactive and Information-Theoretic Secure Verifiable Secret Sharing 中提出的 VSS 方案（ \(g\) 是循环群 \(G\) 的生成元， \(h\) 是 \(G\) 中某元素）：

Dealer 随机选择两个多项式 \[\begin{aligned} f(x) &= a_0 + a_1 x + a_2 x^2 + \cdots a_{t-1} x^{t-1} \\ q(x) &= b_0 + b_1 x + b_2 x^2 + \cdots b_{t-1} x^{t-1}\end{aligned}\] 需要满足条件：秘密值 \(s=f(0)=a_0\) ，任意 \(t\) 个参与者可以恢复出 \(s\) 。
Dealer 计算 \((f(i), q(i))\) ，其中 \(1 \le i \le n\) ，通过加密通道把 \((f(i), q(i))\) 分配给参与者 \(P_i\) 。
Dealer 同时公开下面信息： \[c_i = g^{a_i}h^{b_i}\] 其中 \(0 \le i \le t - 1\) 。这里， \(c_0,c_1,\cdots,c_{t-1}\) 也被称为 commitment。
每个参与者 \(P_i\) 验证自己收到的 \((f(i), q(i))\) ，如果 \[g^{f(i)}h^{q(i)} = c_0 c_1^{i} c_2^{i^2} \cdots c_{t-1}^{i^{t-1}}\] 成立，则通过验证，如果不成立就终止协议。

和 Feldman VSS 不同，Pedersen VSS 具有 Information-Theoretic Secure 属性。

4. Publicly Verifiable Secret Sharing（PVSS）

在前一节介绍的 VSS 中，参与者在校验阶段中都用到了 Dealer 在加密通道中向其发送的数据。这样，对于 VSS 来说，只有参与者才可以校验 Dealer 分发的秘密分片是否正确。

是否可以去掉这个限制，也就是说任何人（不一定是参与者）都可以校验 Dealer 分发的秘密分片是否正确呢？答案是肯定的，这就是 Publicly Verifiable Secret Sharing（PVSS）问题，它由 Stadler 于 1996 年在论文 Publicly Verifiable Secret Sharing 中首先提出。

1999 年，Berry Schoenmakers 在论文 A Simple Publicly Verifiable Secret Sharing Scheme and its Application to Electronic Voting 中给出了性能更好的 PVSS 方案，这里不详细介绍。

5. Asynchronous Verifiable Secret Sharing（AVSS）

在分布式系统中，有下面网络模型：

synchrony：节点发出的消息，在一个确定的时间内，肯定会到达目标节点；这是一种理想情况。
partial synchrony (weak synchrony)：节点发出的消息，虽然会有延迟，但是最终会到达目标节点。
asynchrony：节点发出的消息，可能丢失，不能确定一定会到达目标节点。

对于 Synchronous VSS 模型来说，我们可以简单地等待 \(n\) 个参与者都有确认，只要有参与者没有正常工作就退出整个 Secret Sharing 过程即可。

而对于 Asynchronous VSS 来说，要相当困难一些，因为这种模型下，“节点失败”是必须考虑的场景。假设 \(f\) 是网络中能忍受的最大失败节点数，则只要 \(n-f\) 个节点工作正常，则 Asynchronous VSS 就需要工作正常。

这里不具体介绍 Asynchronous Verifiable Secret Sharing，可参考：Asynchronous Verifiable Secret Sharing and Proactive Cryptosystems, Christian Cachin 2002

6. Distributed Key Generation（DKG）

在 VSS 协议中，都需要一个 Dealer（他掌握着完整的秘密值）参与，有没有不需要 Dealer 参与的秘密值分享算法？答案是有的，它们被称为 Distributed Key Generation（DKG）算法。

有两个使用较广的 DKG 协议：

1991 年，Pedersen 在论文 A Threshold Cryptosystem without a Trusted Party 中提出的，可称为 Pedersen's DKG（又可称为 Joint Feldman DKG，或者简称 JF DKG）。
2006 年，Rosario Gennaro 等在论文 Secure Distributed Key Generation for Discrete-Log Based Cryptosystems 中提出的协议，可称为 Gennaro DKG。这个 Gennaro DKG 和 Pedersen's DKG（Joint Feldman DKG）的主要区别在于：Pedersen's DKG（Joint Feldman DKG）使用了 Feldman VSS，而 Gennaro DKG 使用了 Pedersen VSS。