Wavelet Transform

1. 小波变换简介
- 1.1. 什么是小波和母小波
2. 哈尔小波变换(Haar Wavelet Transform)

1. 小波变换简介

小波变换（小波分析）是一种新兴的数学分支，它是泛函数、Fourier 分析、调和分析、数值分析的最完美的结晶；在应用领域，特别是在信号处理、图像处理、语音处理以及众多非线性科学领域，它被认为是继 Fourier 分析之后的又一有效的时频分析方法。

参考：
“Wavelet Theory: An Elementary Approach with Applications. David K. Ruch, Patrick J. Van Fleet”（强烈推荐该书）

1.1. 什么是小波和母小波

小波(Wavelet)是一组函数，它们是通过母小波(Mother Wavelet)进行“伸缩”和“位移”而得到的。母小波（常用 $ψ (t)$ 表示）是具有特殊性质的实值函数，函数形式是迅速地振荡衰减，且需要满足积分为零（ $\int_{- \infty}^{\infty} ψ (t) d t = 0$ ）等条件。图 1 是母小波的一些例子。小波可以用下面形式表示：
$ψ_{a, b} (t) = \frac{1}{\sqrt{a}} ψ (\frac{t - b}{a})$
其中， $a$ 是缩放因子， $b$ 是平移参数， $ψ (t)$ 是母小波。

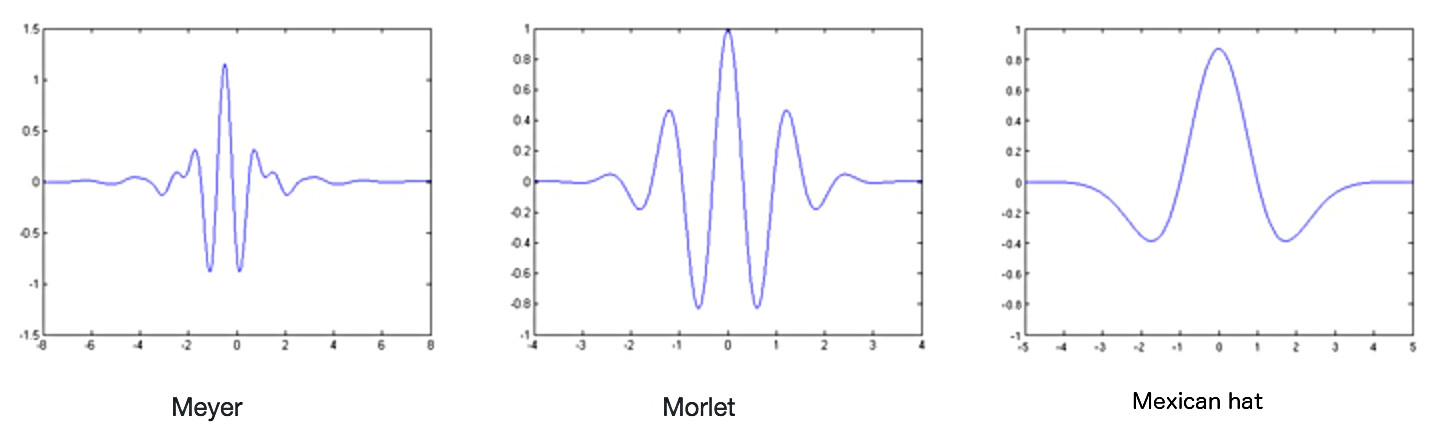
Figure 1: 母小波的一些例子

参考：
Wavelets for kids: A tutorial introduction

2. 哈尔小波变换(Haar Wavelet Transform)

哈尔小波变换(Haar wavelet)是最简单的小波变换。

2.1. 哈尔小波级数展开

哈尔小波级数展开为：
$f (t) = c_{00} φ_{00} (t) + \sum_{j = 0}^{\infty} \sum_{k} d_{j k} ψ_{j k} (t)$
其中，函数 $φ_{00} (t)$ （被称为“尺度函数”）和 $ψ_{j k} (t)$ （被称为“小波函数”，特别地， $ψ_{00} (t)$ 是母小波，常记为 $ψ (t)$ ）如图 2 所示。 $c_{00}$ 和 $d_{j k}$ 的计算公式分别为：
$\begin{aligned} c_{00} = \int_{0}^{1} f (t) φ_{00} (t) d t \\ d_{j k} = \int_{0}^{1} f (t) ψ_{j k} (t) d t \end{aligned}$

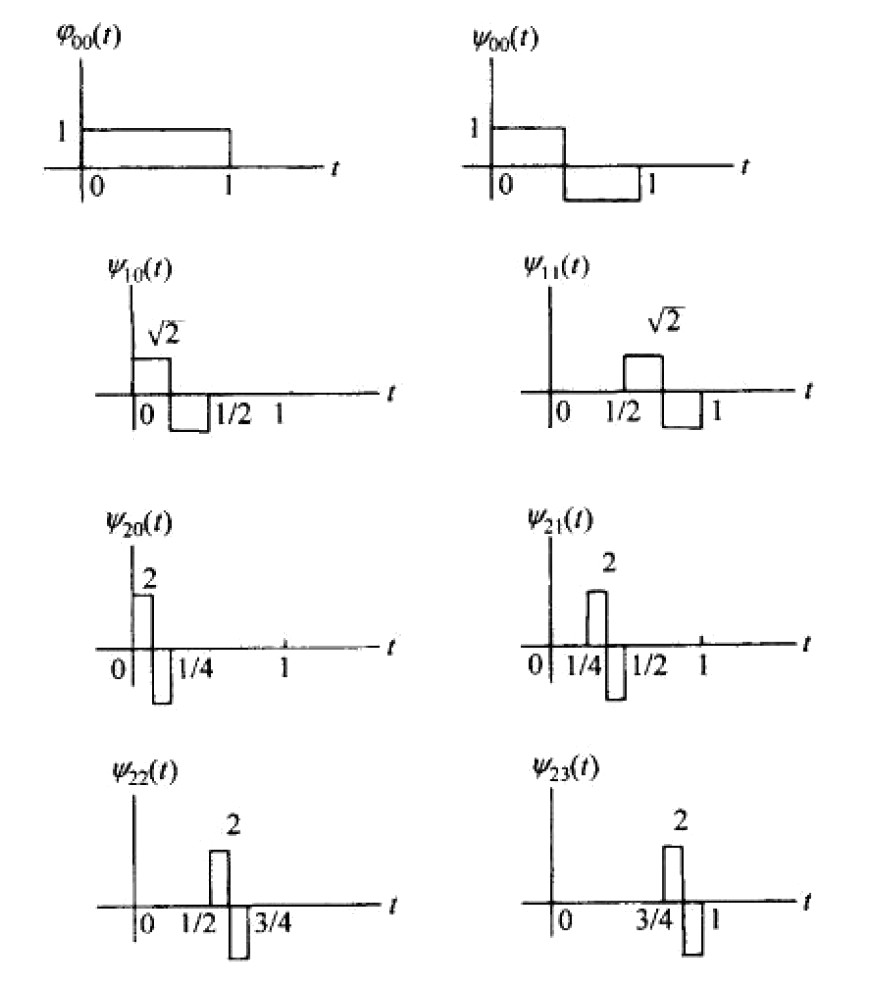
Figure 2: 哈尔尺度函数和第 0 层到第 2 层哈尔小波函数

说明，图 2 中的层数还可以继续增加，每增加一层，小波个数增加一倍（如第 3 层包含 8 个小波），每个小波的长度是前一层小波长度的一半，具体地，可由 $ψ_{j k} (t) = 2^{j / 2} ψ (2^{j} t - k)$ 来决定其他层的哈尔小波。

参考：《小波基础及应用教程》

2.1.1. 实例：求函数的哈尔小波级数展开

求下面函数的哈尔小波级数展开。
$f (t) = {\begin{cases} t^{2}, & 0 \leq t \leq 1 \\ 0, & others \end{cases}$

直接利用前面介绍的公式求解。
$\begin{aligned} c_{00} = \int_{0}^{1} t^{2} φ_{00} (t) d t = \int_{0}^{1} t^{2} d t = \frac{1}{3} \\ d_{00} = \int_{0}^{1} t^{2} ψ_{00} (t) d t = \int_{0}^{0.5} t^{2} d t - \int_{0.5}^{1} t^{2} d t = - \frac{1}{4} \\ d_{10} = \int_{0}^{1} t^{2} ψ_{10} (t) d t = \int_{0}^{0.25} t^{2} \sqrt{2} d t - \int_{0.25}^{0.5} t^{2} \sqrt{2} d t = - \frac{\sqrt{2}}{32} \\ d_{11} = \int_{0}^{1} t^{2} ψ_{11} (t) d t = \int_{0.5}^{0.75} t^{2} \sqrt{2} d t - \int_{0.75}^{1} t^{2} \sqrt{2} d t = - \frac{3 \sqrt{2}}{32} \end{aligned}$
这里，仅计算了第 0 层和第 1 层，得到了 $f (t)$ 的近似展开如图 3 所示。
$f (t) = \frac{1}{3} φ_{00} (t) + [- \frac{1}{4} φ_{00} (t)] + [- \frac{\sqrt{2}}{32} φ_{10} (t) - \frac{3 \sqrt{2}}{32} φ_{11} (t)] + \dots$
为了得到更加精确的表示，还可以计算第 2 层、第 3 层，直到 $\infty$ 层实现精确表示。

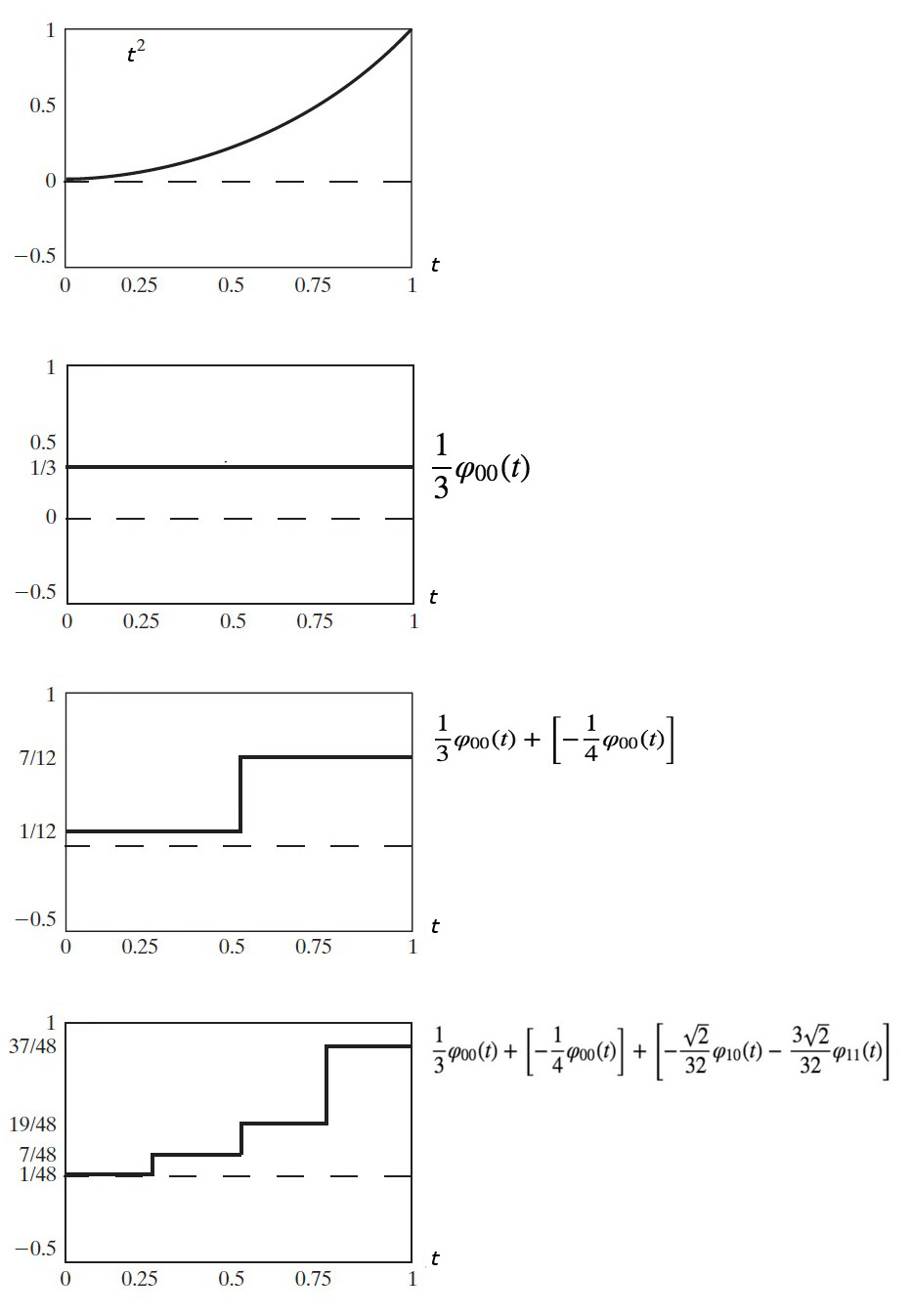
Figure 3: $f (t) = t^{2}$ 的哈尔小波级数展开

注：这个例子摘自《数字图像处理(第三版)冈萨雷斯，7.3 一维小波变换》

2.2. 离散哈尔小波变换

2.2.1. 简单例子

小波变换最常用的应用是信号压缩。我们通过一个简单的例子来说明小波变换。

假设你想发送下面信号（8个数字，可以想像为一幅只有 8 个像素的图像）给你的朋友。

[200, 220, 150, 140, 96, 100, 100, 100]

但由于网络非常慢（这仅是一个例子，网络不至于会慢到如此），你只能发送 4 个数字。你会怎么做呢？直观的想法是 对每两个相邻的数字求平均值，只发送这些平均值。 即发送：

[(200+220)/2, (150+140)/2, (96+100)/2, (100+100)/2] = [210, 145, 98, 100]

你朋友收到这 4 个数字后，无法精确地恢复这 8 个数字，但对信号也有个大致的了解。假设你被允许再发送 4 个数字。你又会怎么做呢？这时，可以 发送相邻的数字的差值除以 2（称为细节系统）。 即发送：

[(200-220)/2, (150-140)/2, (96-100)/2, (100-100)/2] = [-10, 5, -2, 0]

这样，你朋友收到这两次数据后，可以完全地恢复你想要发送的原始信号了。

当然，我们还可以接着分解。如表 1 所示。

分辨率	平均值	细节系数
8	[200, 220, 150, 140, 96, 100, 100, 100]
4	[210, 145, 98, 100]	[-10, 5, -2, 0]
2	[177.5, 99]	[32.5, -1]
1	[138.25]	[39.25]

这就是哈尔小波变换的基本思想。

在上面例子中，哈尔小波变换把 “[200, 220, 150, 140, 96, 100, 100, 100]”转换了“[210, 145, 98, 100, -10, 5, -2, 0]”，这个过程，可以用矩阵来表示。那这个变换矩阵是什么呢？即图 4 中的大问号代表的矩阵会是什么呢？

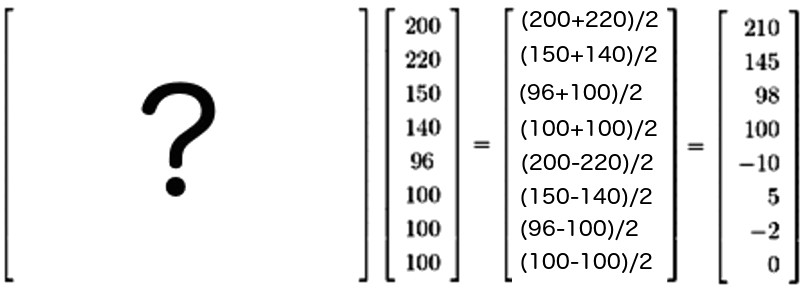
Figure 4: 变换矩阵是什么呢

容易求得大问号代表的哈尔小波变换的“变换矩阵”为下式左边的大矩阵。
$[\begin{array}{cccccccc} 1 / 2 & 1 / 2 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 / 2 & 1 / 2 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 / 2 & 1 / 2 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 / 2 & 1 / 2 \\ 1 / 2 & - 1 / 2 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 / 2 & - 1 / 2 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 / 2 & - 1 / 2 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 / 2 & - 1 / 2 \end{array}] [\begin{matrix} 200 \\ 220 \\ 150 \\ 140 \\ 96 \\ 100 \\ 100 \\ 100 \end{matrix}] = [\begin{matrix} 210 \\ 145 \\ 98 \\ 100 \\ - 10 \\ 5 \\ - 2 \\ 0 \end{matrix}]$

类似地，我们可以求得哈尔小波变换的“逆变换矩阵”为下式左边的大矩阵。
$[\begin{array}{cccccccc} 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & - 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & - 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & - 1 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & - 1 \end{array}] [\begin{matrix} 210 \\ 145 \\ 98 \\ 100 \\ - 10 \\ 5 \\ - 2 \\ 0 \end{matrix}] = [\begin{matrix} 200 \\ 220 \\ 150 \\ 140 \\ 96 \\ 100 \\ 100 \\ 100 \end{matrix}]$

说明：在正式定义哈尔离散小波变换时，一般需要把变换矩阵和逆变换矩阵进行 “规范正交化” 。

参考：
Image Compression: How Math Led to the JPEG2000 Standard, Haar Wavelet Transformation
Building Our Wavelet Transform - Examples

2.2.2. 一维离散哈尔小波变换

把前面介绍例子中的变换矩阵和逆变换矩阵进行规范正交化，并推广到一般情况，可以得到离散哈尔小波变换的正式定义。

假设 $N$ 是偶数，则一维离散哈尔小波变换(Discrete Haar Wavelet Transformation)定义为下面矩阵对应的变换：
$W_{N} = [\begin{matrix} H_{N / 2} \\ G_{N / 2} \end{matrix}] [\begin{array}{ccccccc} \sqrt{2} / 2 & \sqrt{2} / 2 & 0 & 0 & \dots & 0 & 0 \\ 0 & 0 & \sqrt{2} / 2 & \sqrt{2} / 2 & 0 & 0 \\ ⋮ & ⋱ & ⋮ \\ 0 & 0 & 0 & 0 & \dots & \sqrt{2} / 2 & \sqrt{2} / 2 \\ \sqrt{2} / 2 & - \sqrt{2} / 2 & 0 & 0 & \dots & 0 & 0 \\ 0 & 0 & \sqrt{2} / 2 & - \sqrt{2} / 2 & 0 & 0 \\ ⋮ & ⋱ & ⋮ \\ 0 & 0 & 0 & 0 & \dots & \sqrt{2} / 2 & - \sqrt{2} / 2 \end{array}]$
其中， $\frac{N}{2} \times N$ 块 $H_{N / 2}$ 称为 均值块(averages block) ， $\frac{N}{2} \times N$ 块 $G_{N / 2}$ 称为 细节块(details block) 。由于离散哈尔小波变换的变换是正交矩阵，所以它的“逆变换矩阵”等于它的转置矩阵，即 $W_{N}^{- 1} = W_{N}^{T}$ 。

为什么 $H_{N / 2}$ 被称为“均值块”这个名字呢？把它和一个向量相乘（如 $a$ ）即可看出原因。
$\begin{aligned} H_{\frac{N}{2} \times N} a_{N \times 1} & = [\begin{array}{ccccccc} \sqrt{2} / 2 & \sqrt{2} / 2 & 0 & 0 & \dots & 0 & 0 \\ 0 & 0 & \sqrt{2} / 2 & \sqrt{2} / 2 & 0 & 0 \\ ⋮ & ⋱ & ⋮ \\ 0 & 0 & 0 & 0 & \dots & \sqrt{2} / 2 & \sqrt{2} / 2 \end{array}] [\begin{array}{c} a_{0} \\ a_{1} \\ ⋮ \\ a_{N - 2} \\ a_{N - 1} \end{array}] \\ = \sqrt{2} [\begin{array}{c} \frac{a_{0} + a_{1}}{2} \\ \frac{a_{2} + a_{3}}{2} \\ ⋮ \\ \frac{a_{N - 2} + a_{N - 1}}{2} \end{array}] \end{aligned}$
所以， $H_{N / 2}$ 的作用是计算每两个连续值的“平均值”，再乘以一个系数 $\sqrt{2}$ ，故把 $H_{N / 2}$ 被称为“均值块”。

2.2.3. 二维离散哈尔小波变换

设 $A$ 为 $M \times N$ 矩阵（其中 $M$ 和 $N$ 都是偶数）。则 $W_{M} A$ 相当于对 $A$ 的“每一列”应用一维离散哈尔小波变换。下面是一个简单例子，假设 $A_{4 \times 2}$ 为下面矩阵：
$A = [\begin{matrix} 10 & 16 \\ 2 & 24 \\ 9 & 10 \\ 5 & 10 \end{matrix}]$
从而有：
$W_{4} A = \sqrt{2} [\begin{array}{cccc} 1 / 2 & 1 / 2 & 0 & 0 \\ 0 & 0 & 1 / 2 & 1 / 2 \\ 1 / 2 & - 1 / 2 & 0 & 0 \\ 0 & 0 & 1 / 2 & - 1 / 2 \end{array}] [\begin{matrix} 10 & 16 \\ 2 & 24 \\ 9 & 10 \\ 5 & 10 \end{matrix}] = \sqrt{2} [\begin{array}{ccc} 6 & 20 \\ 7 & 10 \\ 4 & - 4 \\ 2 & 0 \end{array}]$

如果把 $A$ 看作是灰度图像，如图 5 所示。

Figure 5: 一个灰度图像 $A$

则进行 $W_{M} A$ 变换后，得到的图像如图 6 所示，其上半部分是对列每连续两像素取均值的图像，下半部分是每列连续两像素取差值的图像。

Figure 6: $W_{M} A$ 相当于对灰度图像 $A$ 每列应用离散哈尔小波变换

类似地， $A W_{N}^{T}$ 相当于对灰度图像 $A$ 每行应用离散哈尔小波变换，如图 7 所示，其左半部分是对行每连续两像素取均值的图像，右半部分是每行连续两像素取差值的图像。

Figure 7: $A W_{N}^{T}$ 相当于对灰度图像 $A$ 每行应用离散哈尔小波变换

一般地，处理时会同时对图像的列和行应用离散哈尔小波变换，如图 8 所示。这就是二维离散哈尔小波变换。

Figure 8: $W_{M} A W_{N}^{T}$ 相当于同时对图像 $A$ 的列和行应用离散哈尔小波变换

矩阵 $A_{M \times N}$ （其中 $M$ 和 $N$ 都是偶数）的二维离散哈尔小波变换的定义为：
$B = W_{M} A W_{N}^{T}$
其中， $W_{M}$ 和 $W_{N}$ 就是前面介绍一维离散哈尔小波时的变换矩阵。

2.2.3.1. 二维离散哈尔小波变换的进一步分析

由前面的定义知， $A$ 的二维离散哈尔小波变换为：
$\begin{aligned} B & = W_{M} A W_{N}^{T} \\ = [\begin{array}{c} H_{M / 2} \\ G_{M / 2} \end{array}] \cdot A \cdot {[\begin{array}{c} H_{N / 2} \\ G_{N / 2} \end{array}]}^{T} \\ = [\begin{array}{c} H_{M / 2} \\ G_{M / 2} \end{array}] \cdot A \cdot [\begin{array}{cc} H_{N / 2}^{T} & G_{N / 2}^{T} \end{array}] \\ = [\begin{array}{c} H_{M / 2} A \\ G_{M / 2} A \end{array}] \cdot [\begin{array}{cc} H_{N / 2}^{T} & G_{N / 2}^{T} \end{array}] \\ = [\begin{array}{cc} H_{M / 2} A H_{M / 2}^{T} & H_{N / 2} A G_{N / 2}^{T} \\ G_{M / 2} A H_{N / 2}^{T} & G_{M / 2} A G_{N / 2}^{T} \end{array}] \\ = [\begin{array}{cc} A & V \\ H & D \end{array}] \end{aligned}$

$A$ 的元素记为 $a_{i, j}$ ，且记 $α_{i j}, β_{i j}, γ_{i j}, δ_{i j}$ 分别为矩阵 $A, V, H, D$ 的元素。通过仔细推导（略），可得：
$\begin{aligned} α_{i j} & = 2 \cdot \frac{a_{2 i - 1, 2 j - 1} + a_{2 i - 1, 2 j} + a_{2 i, 2 j - 1} + a_{2 i, 2 j}}{4} \\ β_{i j} & = 2 \cdot \frac{- (a_{2 i - 1, 2 j - 1} + a_{2 i, 2 j - 1}) + (a_{2 i - 1, 2 j} + a_{2 i, 2 j})}{4} \\ γ_{i j} & = 2 \cdot \frac{- (a_{2 i - 1, 2 j - 1} + a_{2 i - 1, 2 j}) + (a_{2 i, 2 j - 1} + a_{2 i, 2 j})}{4} \\ δ_{i j} & = 2 \cdot \frac{(a_{2 i - 1, 2 j - 1} + a_{2 i, 2 j}) - (a_{2 i - 1, 2 j} + a_{2 i, 2 j - 1})}{4} \end{aligned}$
从而， $A$ 是 $A$ 的一个“近似矩阵”，而 $V$ 体现了“垂直细节”， $H$ 体现了“水平细节”， $D$ 体现了“对角细节”。

所以，二维离散哈尔小波变换又可以形象地表示为图 9 所示。

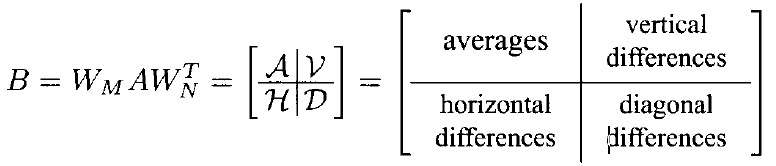
Figure 9: 二维离散哈尔小波变换

参考：
Wavelet Theory, by David K. Ruch, Patrick J. Van Fleet, 4.2 The Two-Dimensional Transform
Discrete Wavelet Transformation - An Elementary Approach with Applications, by Patrick Van Fleet, 6.3 The Two-Dimensional Haar Wavelet Transformation
http://www.whydomath.org/node/wavlets/hwt.html

2.3. 小波变换的应用

JPEG 2000 使用小波变换作为图像的“压缩”算法。小波变换也可用于图像的“边缘检测”。

边缘可以认为是图像中像素的突变，度量变化的基本数字工具是“导数”。小波变换可以得到“导数”的某种近似。

由前面介绍的内容易知，把图像进行二维小波变换后，可分解为四个部分（还可以把 $A$ 继续分解）：
$[\begin{array}{cc} A & V \\ H & D \end{array}]$
分解后，“变化”主要存储在 $V, H, D$ 子矩阵中，如果把子矩阵 $A$ 置为零，再求小波逆变换，得到的主要是差异部分的图像（即图像边缘）。这就是小波变换应用于图像的边缘检测的基本思路。