GMM (Gaussian Mixture Model)
Table of Contents
1. GMM(高斯混合模型)简介
Gaussian Mixture Model 是指多个高斯分布函数的线性组合。
先简单地回顾一下多元高斯分布的定义。对于 \(n\) 维样本空间 \(\mathcal{X}\) 中的随机向量 \(\boldsymbol{x}\) ,若其概率密度函数为:
\[p(\boldsymbol{x}) = \frac{1}{(2\pi)^{n/2} (\det \Sigma)^{1/2}} \exp \left\{ - \frac{1}{2} (\boldsymbol{x} - \boldsymbol{\mu})^{\mathsf{T}} \Sigma^{-1} (\boldsymbol{x} - \boldsymbol{\mu}) \right\}\]
则称 \(\boldsymbol{x}\) 服从高斯分布。其中 \(\boldsymbol{\mu}\) 是 \(n\) 维均值向量, \(\Sigma\) 是 \(n \times n\) 的协方差矩阵, \(\det \Sigma\) 是方阵 \(\Sigma\) 的行列式。从上面式子可知,高斯分布完全由均值向量 \(\boldsymbol{\mu}\) 和协方差矩阵 \(\Sigma\) 这两个参数确定。为了明确显示高斯分布与相应参数的依赖关系,常常将高斯分布的概率密度函数 \(p(\boldsymbol{x})\) 记为 \(p(\boldsymbol{x} \mid \boldsymbol{\mu}, \Sigma)\) 或者 \(\mathcal{N}(\boldsymbol{x} \mid \boldsymbol{\mu}, \Sigma)\) 。
我们可定义 高斯混合分布:
\[\begin{aligned} p_{\mathcal{M}}(\boldsymbol{x}) &= \sum_{k=1}^{K} \pi_k \cdot \mathcal{N}(\boldsymbol{x} \mid \boldsymbol{\mu_k}, \Sigma_k) \\
\sum_{k=1}^{K} \pi_k &= 1, \quad \pi_k > 0 \\
\end{aligned}\]
该分布由 \(K\) 个混合成分(component)组成,每个混合成分对应一个高斯分布。其中 \(\boldsymbol{\mu_k}\) 与 \(\Sigma_k\) 是第 \(k\) 个高斯混合成分的参数,而 \(\pi_k\) 为相应的“混合系数”(mixture coefficient)。
1.1. GMM 用作聚类算法
GMM 用作聚类算法的思想很简单:假设样本数据服从混合高斯分布,根据样本数据集推出混合高斯分布的各个参数,以及各个样本最可能属于哪个高斯分布,这样,GMM 的 \(K\) ( \(K\) 值往往由用户提供)个成分对应于聚类任务中的 \(K\) 个簇,每个样本划到最可能的高斯分布所对应的簇中。 如何根据样本数据求出混合高斯分布的各个参数是关键所在,后面将介绍求解参数的具体过程。
假设 \(K=2\) ,则 GMM 的形式为:
\[\begin{aligned} p_{\mathcal{M}}(\boldsymbol{x}) &= \pi_1 \mathcal{N}(\boldsymbol{x} \mid \boldsymbol{\mu_1}, \Sigma_1) + \pi_2 \mathcal{N}(\boldsymbol{x} \mid \boldsymbol{\mu_2}, \Sigma_2) \\
\pi_1 + \pi_2 &= 1 \\
\end{aligned}\]
2. 使用 EM 算法求解 GMM 中的参数
下面介绍如何通过样本数据求出混合高斯分布的各个参数。
对于高斯混合模型:
\[\begin{aligned} p_{\mathcal{M}}(\boldsymbol{x}) &= \sum_{k=1}^{K} \pi_k \cdot \mathcal{N}(\boldsymbol{x} \mid \boldsymbol{\mu_k}, \Sigma_k) \\
\sum_{k=1}^{K} \pi_k &= 1, \quad \pi_k > 0 \\
\end{aligned}\]
假设样本的生成过程由高斯混合分布给出。高斯混合分布的抽样过程如下:首先,随机地在 \(K\) 个高斯混合成分之中选一个,每个成分被选中的概率是它的系数 \(\pi_k\) ;然后,再单独考虑这个被选择的混合成分,根据它的概率密度函数进行采样,从而生成相应的样本。
若样本集 \(D = \{ \boldsymbol{x_1}, \boldsymbol{x_2}, \cdots, \boldsymbol{x_N} \}\) 由上述过程生成,如何通过样本集估计出模型参数 \(\{(\pi_k, \boldsymbol{\mu_k}, \Sigma_k) \mid 1 \le k \le K \}\) 呢?显然,对于给定的样本集 \(D\) , 如果知道每个样本点是由哪个高斯混合成分生成,则直接采用“极大似然估计”即可求解参数, 即最大化对数似然:
\[\begin{aligned} LL(D) &= \ln \left( \prod_{i=1}^N p_M(\boldsymbol{x_j}) \right) \\
&= \sum_{i=1}^N \ln \left( p_M(\boldsymbol{x_j}) \right) \\
&= \sum_{i=1}^N \ln \left( \sum_{k=1}^{K} \pi_k \cdot \mathcal{N}(\boldsymbol{x} \mid \boldsymbol{\mu_k}, \Sigma_k) \right) \\
\end{aligned}\]
问题在于,对于这个数据集 \(D\) 我们并不知道每个样本点是由哪个高斯混合成分生成(这称为“不完全数据集”),从而无法直接使用极大似然估计来求解参数。这种情况下,我们常用 EM 算法来迭代优化求解。
关于 EM 算法可以参考:http://aandds.com/blog/expectation-maximization.html
2.1. E step
我们引入一个 \(K\) 维随机变量 \(\boldsymbol{z}\) (通常称之为隐含变量,Latent Variable)来描述“样本点是由哪个高斯混合成分生成”这个未知事情,它满足条件: \(z_k \; (1 \le k \le K)\) 只能取 0 或者 1;且 \(\sum_{k=1}^K z_k=1\) 。例如,样本集共有 3 个类别,某一样本点如果它由第 1 个高斯混合成分生成,则相应随机变量 \(\boldsymbol{z} = (1, 0, 0)\) ,如果它由第 2 个高斯混合成分生成,则相应随机变量 \(\boldsymbol{z} = (0, 1, 0)\) ,依此类推 。这样, \(P(z_k = 1)\) 可表示当前样本点由第 \(k\) 个高斯混合成分生成的概率。显然有, \(P(z_k = 1) = \pi_k\) 。
给定样本点 \(\boldsymbol{x_i}\) ,它由第 \(k\) 个高斯混合成分生成的概率(后验概率)为 \(p_M(z_k = 1 \mid \boldsymbol{x_i})\) ,为方便起见把它简记为 \(\gamma_{ik}\) ,由贝叶斯公式和全概率公式知:
注 1:由于“每一类中的样本数据都服从正态分布”,所以有 \(p_M(\boldsymbol{x_i} \mid z_k = 1) = \mathcal{N}(\boldsymbol{x_i} \mid \boldsymbol{\mu_k}, \Sigma_k)\) ,在上式的最后一步推导中利用了这个结论。
注 2:在 \(\gamma_{ik}\) 的计算公式中, \(\pi_k, \boldsymbol{\mu_k}, \Sigma_k\) 是我们需要求解的 3 个参数,是未知的。 采用迭代法,把它们看作已知,也就是取上一次迭代得到的参数值(如果是第 1 次迭代则取其初始值)。
注 3:由于 \(\gamma_{ik}\) 是样本点 \(\boldsymbol{x_i}\) 由第 \(k\) 个高斯混合成分生成的概率,所以, 当迭代结束后,样本点 \(\boldsymbol{x_i}\) 所属的类别 \(\lambda_i\) 由下式确定:
\[\lambda_i = \underset{k \in \{1,2,\cdots, K \}}{\operatorname{arg} \max} \gamma_{ik}\]
注 4:我们还可以用其它隐含变量来描述“样本点是由哪个高斯混合成分生成”这个未知事情,比如 1 维随机变量 \(z\) ,取值为 \(\{1, 2, \cdots, k, \cdots, K\}\) ,取值 \(k\) 时就表示当前样本点由第 \(k\) 个高斯混合成分生成,即有 \(P(z=k) = \pi_k\) 。这样,上面的推导中把 \(z_k = 1\) 换为 \(z=k\) 即可。
2.2. M step
EM 算法是一种迭代算法,在“E step”中求得 \(\gamma_{ik}\) 后,我们要想办法得到参数 \(\pi_k, \boldsymbol{\mu_k}, \Sigma_k\) 的“新估计值”,这样通过这些“新估计值”又可以进行下一轮迭代了。
下面介绍求参数 \(\pi_k, \boldsymbol{\mu_k}, \Sigma_k\) 新估计值的办法(即“M step”)。
前面说过,我们不知道每个样本点是由哪个高斯混合成分生成,从而无法使用极大似然估计来求解参数。但现在情况不同了,我们在“E step”中求得了样本点 \(\boldsymbol{x_i}\) 由第 \(k\) 个高斯混合成分生成的概率(即 \(\gamma_{ik}\) ),数据集 \(D\) 不再是“不完全数据集”了,这样我们可以使用极大似然估计来求解参数 \(\pi_k, \boldsymbol{\mu_k}, \Sigma_k\) 了。
令 \(\frac{\partial LL(D)}{\partial \boldsymbol{\mu_k}} = 0\) 有:
\[ - \sum_{i=1}^N \frac{\pi_k \cdot \mathcal{N}(\boldsymbol{x_i} \mid \boldsymbol{\mu_k}, \Sigma_k)}{\sum_{j=1}^{K} \pi_j \cdot \mathcal{N}(\boldsymbol{x_i} \mid \boldsymbol{\mu_j}, \Sigma_j)} \Sigma_k (\boldsymbol{x_i} - \boldsymbol{\mu_k}) = 0\]
上式中的分式部分和前面推导的 \(\gamma_{ik}\) 计算公式是相同的。利用这点,再把上式重新整理可得到:
上式的含义是各混合成分的均值可通过样本加权平均来估计,样本权重是每个样本属于该成分的后验概率。
类似地,令 \(\frac{\partial LL(D)}{\partial \boldsymbol{\Sigma_k}} = 0\) 可得:
对于混合系数 \(\pi_k\) ,除了要最大化 \(LL(D)\) 外,还需要满足 \(\sum_{k=1}^N \pi_k = 1\) ,我们可以用拉格朗日乘数法来求解这个条件极值问题。其拉格朗日函数为:
\[LL(D) + \lambda \left(\sum_{k=1}^N \pi_k - 1 \right) \]
上式中 \(\lambda\) 是拉格朗日乘子,令上式对 \(\pi_k\) 的导数为 0,再和 \(\sum_{k=1}^N \pi_k = 1\) 联立方程组,有:
\[\begin{cases} \sum_{i=1}^N \frac{\mathcal{N}(\boldsymbol{x_i} \mid \boldsymbol{\mu_k}, \Sigma_k)}{\sum_{j=1}^{K} \pi_j \cdot \mathcal{N}(\boldsymbol{x_i} \mid \boldsymbol{\mu_j}, \Sigma_j)} + \lambda = 0 \\
\sum_{k=1}^N \pi_k = 1 \\
\end{cases}\]
求解上面方程组,得(还可得 \(\lambda=-N\) ,这里不关心它):
上式的含义是每个高斯分成的混合系数由样本属于该成分的平均后验概率确定。
3. GMM 聚类算法
3.1. GMM 聚类算法总结
前面已经完整地介绍过了 GMM 聚类算法。这里总结如图 1 所示。

Figure 1: 高斯混合聚类算法
算法第 1 行对高斯混合分布的模型参数进行初始化。然后,在第 2-12 行基于 EM 算法对模型参数进行迭代更新。若 EM 算法满足停止条件,则在第 14-17 行根据高斯混合分布确定簇划分,在第 18 行返回最终结果。
图 2 是使用 EM 算法更新 GMM 参数( \(K=2\) )的一个例子。
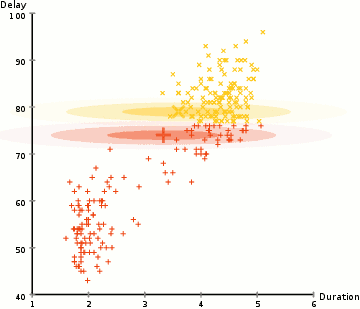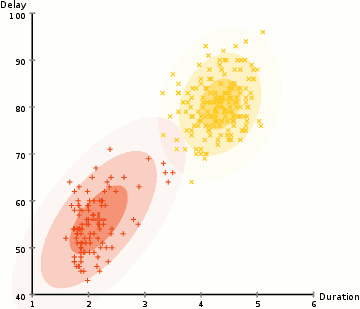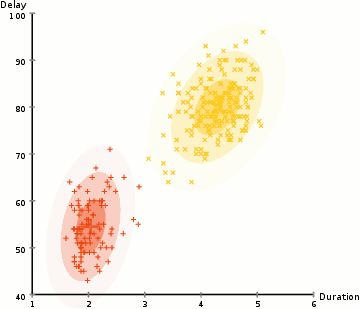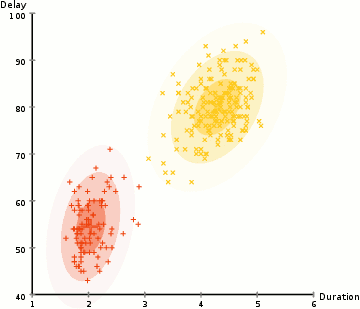
Figure 2: 使用 EM 算法更新 GMM 参数的 gif 动画演示,摘自https://brilliant.org/wiki/gaussian-mixture-model/
3.2. GMM 应用实例
以图 3 所示的西瓜相关数据集为例,令高斯混合成分个数 \(K=3\) 。请用 GMM 聚类算法进行聚类处理。
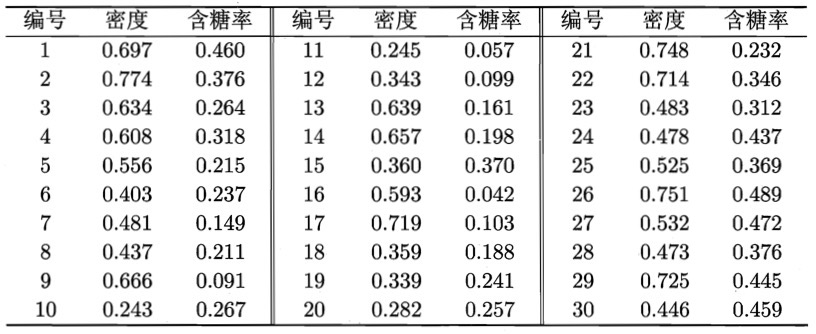
Figure 3: 西瓜数据集
算法开始时,将高斯混合分布的模型参数初始化为 \(\pi_1 = \pi_2 = \pi_3 = \frac{1}{3}; \boldsymbol{\mu_1} = \boldsymbol{x_6}, \boldsymbol{\mu_2} = \boldsymbol{x_{22}}, \boldsymbol{\mu_3} = \boldsymbol{x_{27}}; \Sigma_1 = \Sigma_2 = \Sigma_3 = \left( \begin{array}{cc} 0.1 & 0.0 \\ 0.0 & 0.1 \end{array} \right)\)
在第一轮迭代中,先计算样本由各混合成分生成的后验概率。以 \(\boldsymbol{x_1}\) 为例,由“E step”的公式算出后验概率 \(\gamma_{11} = 0.219, \gamma_{12} = 0.404, \gamma_{13} = 0.377\) 。所有样本的后验概率算完后,由“M step”的 3 个公式可得到如下新的模型参数:
\[\begin{align*} & \pi_1' = 0.361, \pi_2' = 0.323, \pi_3' = 0.316 \\
& \boldsymbol{\mu_1'} = (0.491; 0.251), \boldsymbol{\mu_2'} = (0.571; 0.281), \boldsymbol{\mu_3'} = (0.534; 0.295) \\
& \Sigma_1' = \left( \begin{array}{cc} 0.025 & 0.004 \\ 0.004 & 0.016 \end{array} \right), \Sigma_2' = \left( \begin{array}{cc} 0.023 & 0.004 \\ 0.004 & 0.017 \end{array} \right), \Sigma_3' = \left( \begin{array}{cc} 0.024 & 0.005 \\ 0.005 & 0.016 \end{array} \right) \\
\end{align*}\]
模型参数更新后,不断重复上述过程,不同轮数之后的聚类结果如图 4 所示。
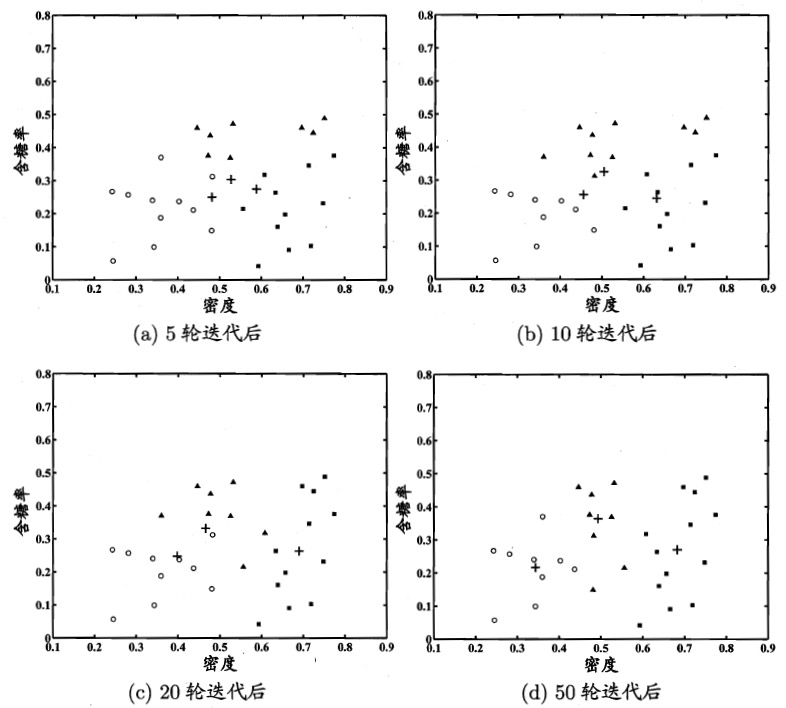
Figure 4: 高斯混合聚类( \(K=3\) )在不同轮数迭代后的聚类结果。其中样本簇 \(C_1,C_2,C_3\) 中的样本点分别用“○”,“■”与“▲”表示,各高斯混合成分的均值向量用“+”表示
3.3. GMM vs. K-means 算法
GMM 和 K-means 算法都是迭代算法,迭代策略类似:先对参数赋初值,然后交替执行两个步骤,一个步骤是对数据的估计(K-means 是每个点所属簇,GMM 是隐含变量的期望);另一个步骤是用上一步算出的估计值重新计算参数值,更新待估计参数(K-means 是簇心位置,GMM 是混合系数和各个高斯分布的中心位置和协方差矩阵)。
和 K-means 聚类算法不同(它直接给出样本点的类别),GMM 还可以给出某个样本点属于某个类别的概率,这种方式提供的信息量显然更多。
4. 参考
本文主要摘自:《机器学习,周志华,2016》,9.4.3,高斯混合聚类
Christopher M. Bishop etc., Pattern Recognition and Machine Learning, Chapter 9 Mixture Models and EM