Reinforcement Learning
Table of Contents
1. Model-free Learning
强化学习一般使用马尔可夫决策过程(Markov Decision Processes, MDP)来描述。在强化学习中,如果环境的转移模型,回报函数是已知的,这被称为“有模型学习”(model-based learning)。对于 model-based learning,求解最优策略有两种常用方法:“价值迭代”和“策略迭代”。在阅读下面内容前请先熟悉 model-based learning,如果不熟悉可参考:http://aandds.com/blog/mdp.html
在很多时候,环境的转移模型,回报函数是很难得到的,甚至很难知道环境中一共有多少状态,这被称为“免模型学习”(model-free learning)。后文介绍的“蒙特卡罗”和“时序差分”都属于 model-free learning。
2. 蒙特卡罗(Monte Carlo)强化学习
在 model-free 情况下,转移模型等是未知的。蒙特卡罗方法又称为模拟统计方法,它不需要模型的定义,适用于 model-free 的情况。
2.1. 策略评估
假设我们选择了一个策略 \(\pi\) ,那么怎么评估它好不好呢?
蒙特卡洛是一种模拟统计方法,当模型未知(model-free)时,对策略 \(\pi\) 进行多次采样(每次采样称为一个Episode),每次采样从开始状态开始(记为 \(s_0\) ),到终止状态结束(记为 \(s_T\) ),如:
\[\langle S_0, A_0, R_1, S_1, A_1, R_2, \cdots, S_t, A_t, R_{t+1}, \cdots, S_{T-1}, A_{T-1}, R_T, S_T \rangle\]
设某次采样得到的状态轨迹为 \(s_0, s_1, \cdots, s_T\) ,在这个轨迹下依次得到的回报为 \(r_1, r_2, \cdots, r_T\) 。在第 \(k\) 次采样中,把状态 \(s_t\) (第 \(k\) 次采样中 \(t\) 时刻的状态)的折扣回报记为 \(G_k(s_t)\) ,根据折扣回报的定义,它的计算公式如下:
\[G_k(s_t) = r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3} + \cdots +\gamma^{T-1} r_{T}\]
\(G_k(s_t)\) 的含义是跟随 \(s_t\) 出现的状态序列的折扣回报。
下面用一个实例来介绍一下 \(G_k(s_t)\) 的计算。假设在策略 \(\pi\) 下,前两次采样得到下面序列( \(s_0\) 是开始状态, \(s_8\) 和 \(s_7\) 是终止状态,状态中间的数字表示即时回报):
\[\begin{align*} & s_0, +1, s_3, +1, s_4, +5, s_8 \\
& s_0, +0, s_4, +0, s_2, +4, s_6, +3, s_7 \end{align*}\]
如果 \(\gamma = 1\) ,则对于状态 \(s_4\) 来说,前两次采样的折扣回报分别为:
\[\begin{align*} G_1(s_4) &= 5 \\
G_2(s_4) &= 0 + 1 \times 4 + 1^2 \times 3 = 7 \end{align*}\]
蒙特卡洛方法采用的办法是 用 \(k\) 次采样中 \(G_k\) 的平均值来估计状态 \(s\) 的价值, 即:
前面例子中,在策略 \(\pi\) 下进行两次采样后可以估计状态 \(s_4\) 的价值为 \(V_2(s_4) = (5+7)/2 = 6\) 。
由大数定理知,当采样次数足够多( \(k \to \infty\) )时,上式就是在策略 \(\pi\) 下,状态 \(s\) 的价值,即:
\[\lim_{k \to \infty}V_k(s) = V^{\pi}(s)\]
2.1.1. 增量更新
计算 \(V_k(s)\) 时,为了避免存储所有的回报,可以把它改写为“增量更新”的形式,推导如下:
\[\begin{align*} V_{k+1}(s) & = \frac{G_1(s) + G_2(s) + \cdots + G_{k+1}(s)}{k+1} \\
& = \frac{ k V_k(s) + G_{k+1}(s)}{k+1} \\
& = \frac{1}{k+1} \left[ (k+1) V_k(s) - V_k(s) + G_{k+1}(s) \right] \\
& = V_k(s) + \frac{1}{k+1} \left[ G_{k+1}(s) - V_k(s) \right] \end{align*}\]
由上式知,计算 \(V_{k+1}(s)\) 时只需要记下 \(V_{k}(s)\) 和 \(k\) ,不再需要记录 \(G_1(s), G_2(s), \cdots, G_k(s)\) 了。更进一步,我们可以连 \(k\) 都不用记录:
其中, \(\alpha\) 为正数,它随着采样数 \(k\) 的增加而不断变小。 \(G_{k+1}(s) - V_k(s)\) 可以看作是估计误差。
2.1.2. First Visit VS. Every Visit
在一次 episode 过程中,同一个状态可能出现多次。假设在第 3 次 episode 时出现下面序列:
\[s_0, +0, s_4, +0, s_2, +4, s_6, +1, s_4, +1, s_5, +2, s_7\]
上面出现了两次状态 \(s_4\) ,那么这第一个和第二个状态 \(s_4\) 的折扣回报分别为:
First Visit 的含义是在计算状态 \(s\) 处的值函数时,只利用每次实验(episode)中第一次访问到状态 \(s\) 时返回的值,如前面例子中计算 \(V(s_4)\) 时只使用 \(G_{31}(s_4)\) 。
Every Visit 的含义是在计算状态 \(s\) 处的值函数时,利用所有访问到状态 \(s\) 时的回报返回值。如前面例子中计算 \(V(s_4)\) 时同时使用 \(G_{31}(s_4)\) 和 \(G_{32}(s_4)\) 。
2.1.3. 优缺点
Monte Carlo Methods have below advantages:
- Zero bias
- Good convergence properties (even with function approximation)
- Not very sensitive to initial value
- Very simple to understand and use
But it has below limitations as well:
- MC must wait until end of episode before return is known
- MC has high variance
- MC can only learn from complete sequences
- MC only works for episodic (terminating) environments
参考:https://towardsdatascience.com/monte-carlo-learning-b83f75233f92
2.2. epsilon-greedy 策略
要较好地获得值函数的估计,我们需要多条不同的采样轨迹。然而,我们的策略有可能是确定性的,即对于某个状态只会输出一个动作,若使用这样的策略进行采样,则只能得到多条相同的轨迹。
为了解决这问题,我们以 \(\epsilon\) 的概率从所有动作中均匀随机选取一个,以 \(1-\epsilon\) 的概率选取当前最优动作。我们将确定性的策略 \(\pi\) 称为“原始策略”,在原始策略上使用 epsilon-greedy 的策略记为:
\[\pi^{\epsilon} = \begin{cases}
\pi(x), & \text{以概率} 1 - \epsilon \\
A \text{中以均匀概率选取的动作}, & \text{以概率} \epsilon \\
\end{cases}\]
本文介绍的策略都是 epsilon-greedy策略。
3. 时序差分(Temporal Difference)强化学习
前面介绍 Monte Carlo 强化学习时,推导出了“状态-值函数”的增量更新公式:
\[V_{k+1}(s_t) = V_{k}(s_t) + \alpha [G_{k+1}(s_t) - V_{k}(s_t)]\]
\(G_{k+1}(s_t)\) 表示在第 \(k+1\) 个Episode中,在状态 \(s_t\) 之后出现的状态序列的折扣回报。根据其定义知,计算 \(G_{k+1}(s_t)\) 时必须是第 \(k+1\) 次采样时按照某个策略执行到一个“终止状态 \(s_T\) ”。也就是说根据某一策略转移到了下一个状态,这时还不能马上更新“状态-值函数”,需要等待这次模拟执行到一个“终止状态”才能计算 \(G_{k+1}(s_t)\) ,才能更新“状态-值函数”。
下面我们想办法来解决这个“痛点”,即去掉必须模拟执行到“终止状态”才能计算 \(G_{k+1}(s)\) 的限制。
假定 \(\gamma=1\) ,则代入定义 \(G_{k+1}(s_t) = r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3} + \cdots +\gamma^{T-1} r_{T}\) 后,有:
\[V_{k+1}(s_t) = V_{k}(s_t) + \alpha [r_{t+1} + r_{t+2} + \cdots + r_T - V_{k}(s_t)]\]
设 \(V_k(s_{T}) = 0\) (到终止状态 \(s_T\) 后不会再转移了,可以认为跟随 \(s_T\) 出现的状态序列不再有回报),再利用 \(\gamma=1\) ,上式可改写为:
\[\begin{align*} V_{k+1}(s_t) = V_{k}(s_t) + \alpha \big( &(r_{t+1} + \gamma V_k(s_{t+1}) - V_k(s_t)) \\
&+ (r_{t+2} + \gamma V_k(s_{t+2}) - V_k(s_{t+1})) \\
&+ \cdots \\
&+ (r_{T} + \gamma V_k(s_{T}) - V_k(s_{T-1})) \big) \end{align*}\]
这样改写后,误差( \(\alpha\) 后面的部分)被拆为了 \(T-1\) 份。我们观察第一份误差 \(r_{t+1} + \gamma V_k(s_{t+1}) - V_k(s_t)\) ,发现它在进行 \((s_t, r_{t+1}, s_{t+1})\) 的状态转移后立刻可以计算出来( \(V_k(s_{t+1})\), \(V_k(s_t)\) 是第 \(k\) 轮模拟对 \(s_{t+1}\), \(s_t\) 的估计,它们在上轮估计中的值,现在都在进行第 \(k+1\) 轮模拟了),第二份误差 \(r_{t+2} + \gamma V_k(s_{t+2}) - V_k(s_{t+1})\) 则在进行 \((s_{t+1}, r_{t+2}, s_{t+2})\) 的状态转移后可以计算出来,依此类推。
如果我们仅保留第一份误差,省略其它误差。这样在进行 \((s_t, r_{t+1}, s_{t+1})\) 的状态转移后我们就可以立刻对 \(V(s_t)\) 进行新的估计了。从而去掉必须模拟执行到“终止状态”才能计算 \(G(s)\) 的限制,这就是时序差分强化学习的思想。 即:
\[V(s_t) \leftarrow V(s_t) + \alpha [r_{t+1} + \gamma V(s_{t+1}) - V(s_t)]\]
上面省略了迭代计算的轮次 \(k\) ,每次都写上它有点啰嗦,记住 \(\leftarrow\) 右边的 \(V\) 是上次的迭代值,而左边是当前迭代值即可。
Monte Carlo 方法需要往后模拟执行,直到达到终止状态,而上面介绍的时序差分方法是仅往后模拟执行一步,当然我们也可以往后模拟执行 \(n\) 步,这称为 n-step 时序差分学习,如图 1 所示(图片摘自:RL Course by David Silver, Lecture 4: Model-Free Prediction)

Figure 1: n-step temporal difference learning
3.1. TD(0)算法
TD(0)算法前面已经介绍了, \(V(s_t)\) 的迭代更新公式为:
3.2. SARSA算法
SARSA (State–Action–Reward–State–Action) 算法是 Rummery 和 Niranjan 在 1994 年发表的。
3.2.1. Q (Action-value function)
有了“状态-值函数”,为什么需要定义 Q 函数(“行为-值函数”)呢?
However, we must note that knowing the exact value of all states is not enough to determine what to do. If the agent does not know which action results in reaching any particular state, i.e. if the agent does not have a model of the transition function, knowing V does not help it determine its policy. This is why similar algorithms based on state-action pairs and computing the action-value function Q were developed.
摘自:Markov Decision Processes in Artificial Intelligence, 2.5. Temporal difference methods
我们知道,策略 \(\pi\) 下,在状态 \(s\) 处的累积回报的期望值被定义为值函数(或者称为“状态-值函数”),常常用 \(V\) 表示。相应的,策略 \(\pi\) 下,在状态 \(s\) 处执行动作 \(a\) 后的累积回报的期望值被定义为“行为-值函数”,常常用 \(Q\) 表示。
“行为-值函数”的计算公式(也可称为定义)为:
式中, \(r(s, a)\) 表示从状态 \(s\) 处执行动作 \(a\) 后得到的回报, \(p(s' \mid s, a)\) 表示当在状态 \(s\) 中完成行动 \(a\) 时,到达状态 \(s'\) 的概率。
它们显然有关系( \(\pi^*\) 为最优策略):
\[V^{\pi^*}(s) = \max_a Q^{\pi^*}(s, a)\]
3.2.2. 更新公式
SARSA 算法的更新公式和 TD(0) 算法是一样的,只是把“状态-值函数”换成了“行为-值函数”。
SARSA 算法的更新公式:
使用更新公式时需要的信息为 \(s_t, a_t, r_{t+1}, s_{t+1}, a_{t+1}\) ,这也是 SARSA 名称的由来。
SARSA 算法的描述如图 2 所示。

Figure 2: SARSA
摘自:Reinforcement Learning - An Introduction, Chapter 6 Temporal-Difference Learning
3.3. Q-Learning
Q-Learning 算法是 Watkins 在 1989 年发表的,不过直到 1992 年其收敛性才由 Watkins 和 Dayan 证明。
3.3.1. 更新公式
Q-Learning 算法的更新公式和 SARSA 算法是一样的,只是把 \(Q(s_{t+1}, a_{t+1})\) 换成了 \(\max_b Q(s_{t+1}, b)\) (注:行动 \(b\) 是使得 \(Q(s_{t+1}, b)\) 取得最大值的行动,在图 3 中行动 \(b\) 写为了 \(a\) ,它可以写为任何其它符号)。
Q-Learning 算法的更新公式:
Q-Learning 算法的描述如图 3 所示。

Figure 3: Q-learning
3.3.2. 应用实例
3.3.3. SARSA VS. Q-Learning
SARSA 和 Q-Learning 的区别如图 4 所示。
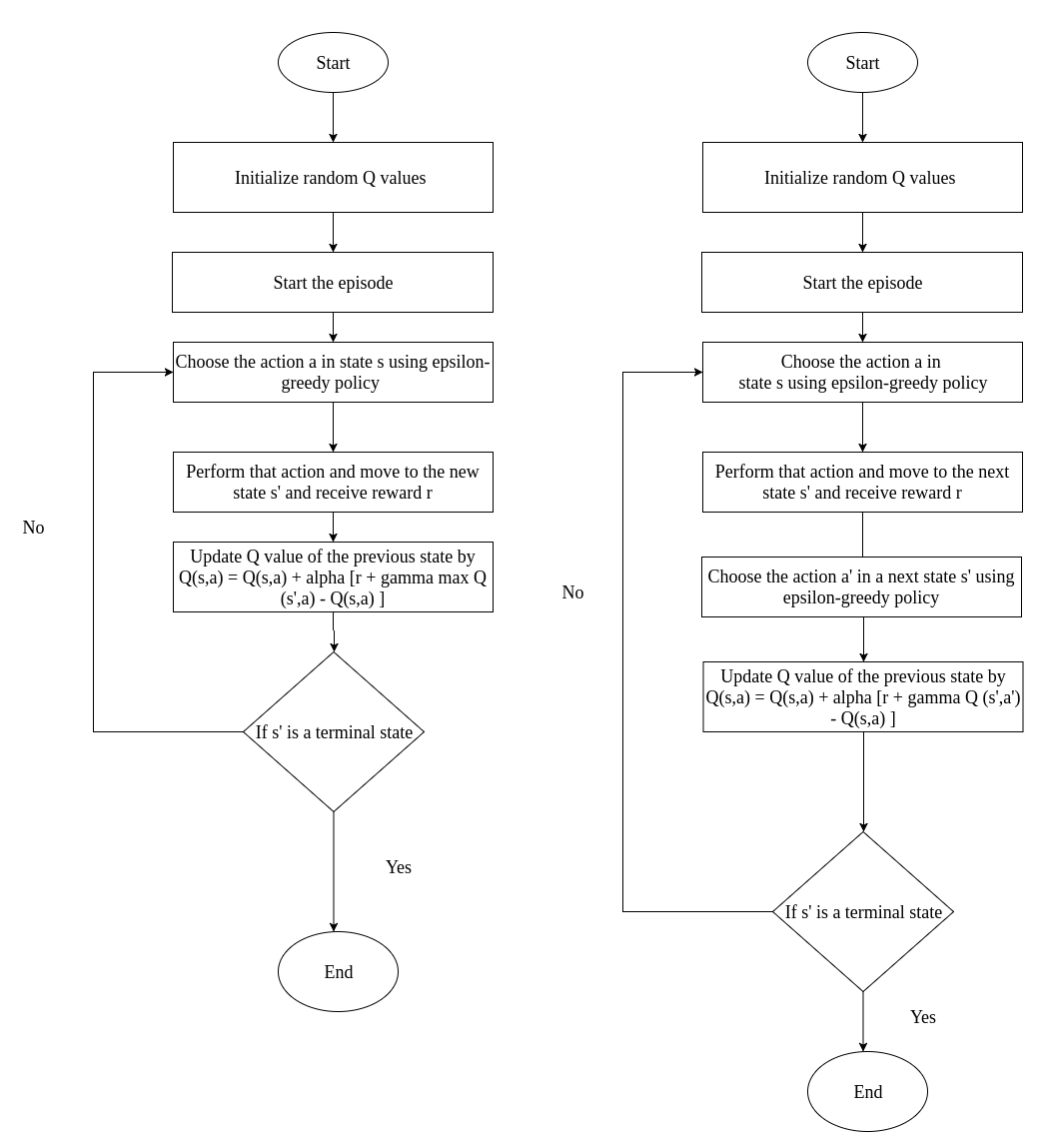
Figure 4: Q-Learning(左图) VS. SARSA(右图)
3.4. Deep Q-Learing (DQN)
深度增强学习(Deep Reinforcement Learning)是 DeepMind 重点研究且发扬光大的机器学习算法框架。DQN(Deep Q-Learning Network)是深度强化学习的开山之作,是将深度学习与强化学习结合起来从而实现从感知(Perception)到动作(Action)的端对端学习的一种全新的算法。比如,利用 DQN 来训练玩 FlappyBird 游戏的话,其输入可以直接是一个个游戏画面。
DQN 由 DeepMind 在 NIPS 2013 上首次发表,后又在 Nature 2015 上发表改进版。后续又有 Double DQN,Prioritised Replay,Dueling Network 等进一步改进。
4. 策略梯度(Policy Gradient Method)
前面介绍的 Q-Learing, DQN 等方法需要计算状态价值函数 V 或者行动价值函数 Q ,被称为 Value Based 方法。
Policy Gradient Method 是另一类强化学习方法,它属于 Policy Based 方法。Actor-Critic 是 Value Based 方法和 Policy Based 方法的结合体。这里不详情介绍它们,请参阅其它书籍。
5. 附录
5.1. 关于记号的说明
从状态 \(s_t\) ,采取行动 \(a_t\) 后转换到状态 \(s_{t+1}\) 得到的回报有两种记法:第一种是记为 \(R(s_t)\) (后面称为记法一),第二种是记为 \(R_{t+1}\) (后面称为记法二)。
5.1.1. 记法一
在 Markov Decision Processes in Artificial Intelligence 一书中采用了记法一。这种记法下“状态-值函数”和“行为-值函数”分别定义如下。
策略 \(\pi\) 下,状态 \(s\) 处的累积回报的期望值被定义为值函数,即“状态-值函数”为:
策略 \(\pi\) 下,状态 \(s\) 进行行动 \(a\) 的价值,即“行为-值函数”为:
5.1.2. 记法二
在 Reinforcement Learning - An Introduction 一书中采用了记法二。这种记法下“状态-值函数”和“行为-值函数”分别定义如下。
假设采样轨迹为:
\[S_0, A_0, R_1, S_1, A_1, R_2, S_2, A_2, R_3, \cdots\]
状态 \(S_t\) 后的回报为 \(R_{t+1}, R_{t+2}, \cdots\) ,这个序列的折扣回报为:
\[G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots = \sum_{k=0}^{\infty} \gamma^k R_{t+k+1}\]
策略 \(\pi\) 下,状态 \(s\) 处的累积回报的期望值被定义为值函数,即“状态-值函数”为:
策略 \(\pi\) 下,状态 \(s\) 进行行动 \(a\) 的价值,即“行为-值函数”为:
5.2. 参考
Markov Decision Processes in Artificial Intelligence
Reinforcement Learning - An Introduction