Convolutional Neural Network

Table of Contents

1. 卷积神经网络简介

卷积神经网络(CNN)是全连接前馈神经网络的特殊情况。CNN 常用于图像处理。

学习 CNN 前，请先理解全连接前馈神经网络，若不理解它，可以参考http://aandds.com/blog/neural-network.html 和 http://aandds.com/blog/neural-network-bp.html。 由于 CNN 常用在图像处理中，理解数字图像处理中的“空间滤波”对学习 CNN 非常有帮助，若不理解它，可以参考http://aandds.com/blog/dip.html。

参考：
An Intuitive Explanation of Convolutional Neural Networks: https://ujjwalkarn.me/2016/08/11/intuitive-explanation-convnets/
Stanford CS231n: Convolutional Neural Networks for Visual Recognition: http://vision.stanford.edu/teaching/cs231n/syllabus.html
Deep Learning, by Ian Goodfellow and Yoshua Bengio and Aaron Courville: http://www.deeplearningbook.org/
神经网络与深度学习讲义（邱锡鹏）

1.1. 卷积层

卷积神经网络是受生物学上接受域(Receptive Field)的机制而提出的。接受域主要是指听觉系统、本体感觉系统和视觉系统中神经元的一些性质。比如， 在视觉神经系统中，一个神经元的接受域是指视网膜上的特定区域，只有这个区域内的刺激才能够激活该神经元。受此启发，CNN 采用了稀疏连接(Sparse Connectivity)的方式（稀疏连接也可称为稀疏权重(Sparse weights)），这相对于全连接前馈神经网络大大减少了计算。 如图 1 所示。

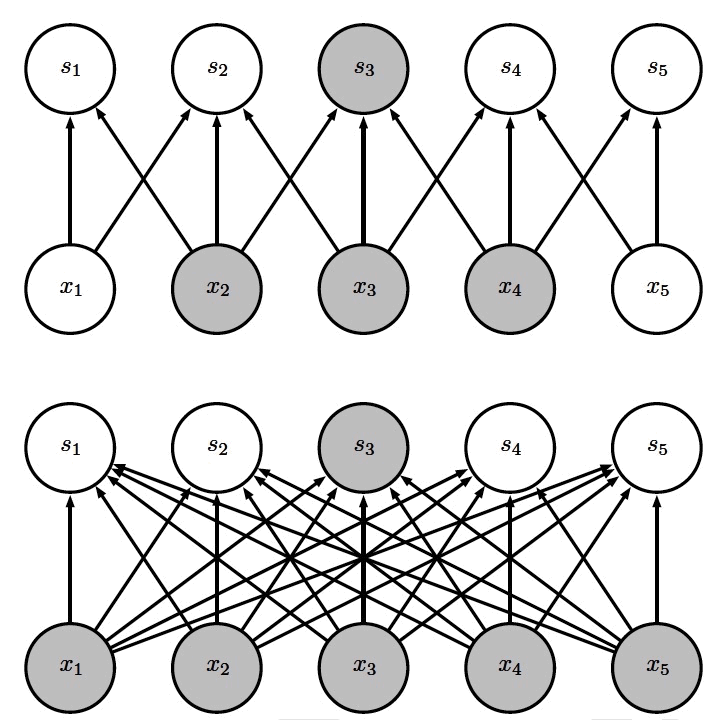
cnn_sparse_conn.gif

Figure 1: 上图演示了 CNN 中的稀疏连接（上图中 \(x_2,x_3,x_4\) 称为 \(s_3\) 的接受域），下图是全连接

在深度卷积网络中，处于卷积网络更深的层中的单元可能与绝大部分输入是间接连接的，如图 2 所示。

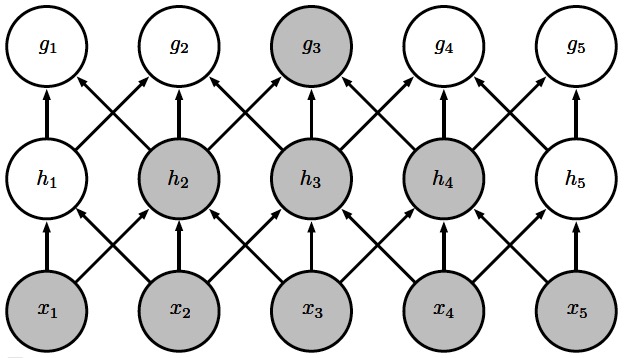
cnn_receptive_field.jpg

Figure 2: 网络深层单元的接受域要比浅层单元的接受域更大

1.1.1. 参数共享

参数共享是指在一个模型的多个函数中使用相同的参数。

在传统的全连接神经网络中，当计算某一层的输出时，神经元参数乘以输入元素后，经过激活函数处理后就作为下一层的输入了，在这个过程中神经元参数只使用了一次，且输出也只是一个值。图 3 （图片摘自：https://ujjwalkarn.me/2016/08/09/quick-intro-neural-networks/ ）演示了使用全连接神经网络识别数字 5 的过程。输入数据维度为 784（28x28 的灰度图片），第一层神经元为 300 个，第二层神经元为 100 个，输出层维度为 10（0 到 9 的数字）。

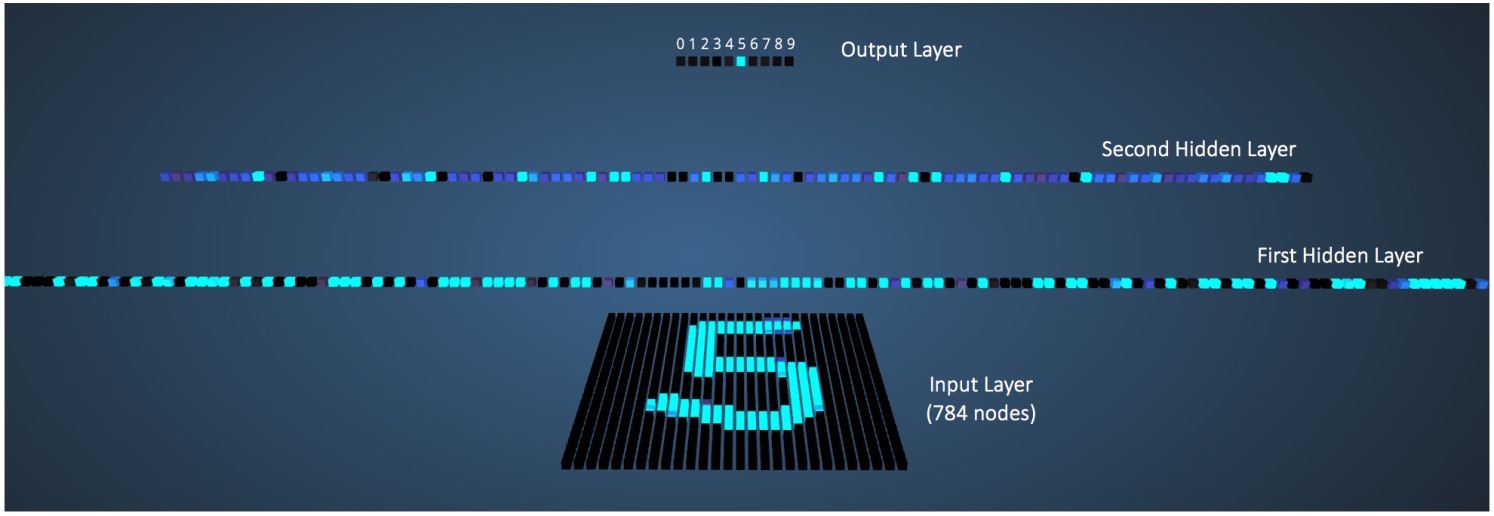
cnn_mlp_example.jpg

Figure 3: 全连接神经网络识别数字 5

而在 CNN 中，一个神经元只会关联到部分输入元素上（稀疏连接）。这时我们让这个神经元应用到输入元素的每一位置上（卷积过程），这个过程中同一个神经元参数被多次使用（每使用一次就得到一个输出值）。显然，“同一个神经元参数被多次使用”也可以看作是“多个神经元使用相同的参数”，这就是“参数共享”名字的由来。在 CNN 中，一般把神经元称为 Filter（或者 Kernel），而使用参数共享后，得到的多个输出值称为 Feature Map（或者称为 Convolved Feature 或 Activation Map）。

在 CNN 的同一层中，可以使用多个 Filter 来得到多个 Feature Map。图 4 采用动画的形式演示了使用两个 Filter 对一个灰度图像进行处理得到两个 Feature Map 的过程。

cnn_feature_maps.gif

Figure 4: 输入图像应用两个 Filter（输入图像中运动的红框和绿框）得到两个 Feature map

图 5 演示了使用 CNN 识别数字 8 的过程。输入数据维度为 1024（32x32 的灰度图片），这里只关注图中的 Convolution Layer 1，这一层有 6 个 Filter（大小为 5×5），输出是 6 个 Feature Map。

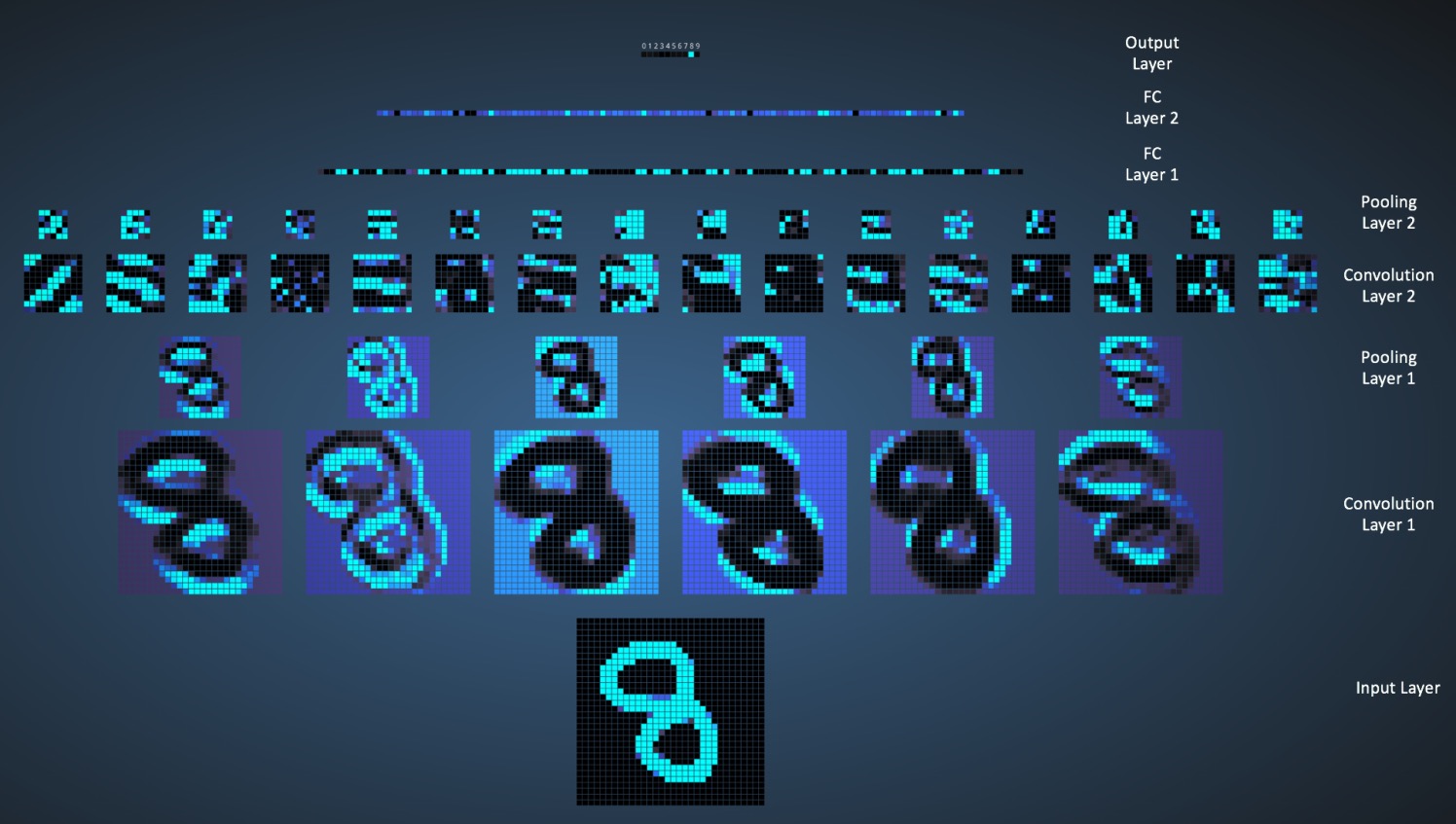
cnn_recognize_8.jpg

Figure 5: CNN 识别数字 8

需要说明的是， 在传统的数字图像处理中，Filter 需要人为给出，如用于边缘检测的 Sobel Filter ；而在 CNN 中，Filter 是在训练阶段中学习而来的。这是神经网络巨大的优势：不用指定 Filter（通过学习而来）就能进行 Feature 提取。 人们往往无法直接理解在 CNN 训练过程中学习到的 Filter，不过，这看起来不是很重要，只要 CNN 能对新数据正确分类即可。

在卷积神经网络的第一层进行边缘检测是很有用的。相同的边缘或多或少地散落在图像的各处，所以应当对整个图像进行参数共享。 但在某些情况下，我们并不希望对整幅图进行参数共享。 例如，在处理已经通过剪裁而使其居中的人脸图像时，我们可能想要提取不同位置上的不同特征（处理人脸上部的部分网络需要去搜寻眉毛，处理人脸下部的部分网络就需要去搜寻下巴了）。

1.1.2. 卷积层的配置参数


卷积层有下面几个重要配置参数：
(1) Filter 的大小。它控制接受域的大小。
(2) Depth（深度）。它表示使用的 Filter 的个数，也就是输出 Feature Map 的个数。如图 5 中 Convolution Layer 1 的 Depth 为 6。
(3) Stride（步幅）。这个概念前面没有介绍。以图像处理为例，它表示卷积运算时（在输入数据上应用 Filter 时）每次跳过的像素个数，为大于等于 1 的整数。显然， 步幅越大，产生的 Feature Map 会越小。
(4) Zero-padding（补零）。通过在输入单元周围补零可改变输入单元大小，从而控制 Feature Map 大小。

1.1.3. 激活函数 (ReLU)

神经元激活函数可以使用传统的 Sigmoid 系列函数（如 logistic 函数，tanh 函数等等）。不过，在实践中使用 Rectified Linear Units (ReLU)比较多。 生物神经学研究表明大脑同时被激活的神经元很少，神经元工作具有稀疏性。ReLU 也具有“稀疏激活性”特点。

ReLU 的函数形式为 \(f(x)=\max(0,x)\) （把小于零的值替换为零），如图 6 中蓝线所示。

cnn_relu.jpg

Figure 6: 蓝线是 ReLU 函数，绿线是 Softplus 函数（它没有“稀疏激活性”）

1.2. 子采样层

一般，卷积层虽然可以显著减少连接的个数，但是每一个特征映射的神经元个数并没有显著减少。这样，如果后面接一个分类器，分类器的输入维数依然很高，很容易出现过拟合。为了解决这个问题， 在 CNN 中一般会在卷积层之后再加上一个池化（Pooling）操作，也就是子采样（Subsampling），构成一个子采样层。子采样层可以来大大降低特征的维数，避免过拟合。 不一定在每个卷积层后都有子采样层，有时连续几个卷积层后才有一个子采样层。

子采样一般有两种方式：取区域内的最大值（Maximum Pooling）或平均值（Average Pooling）。图 7 演示了 Maximum Pooling 的过程。

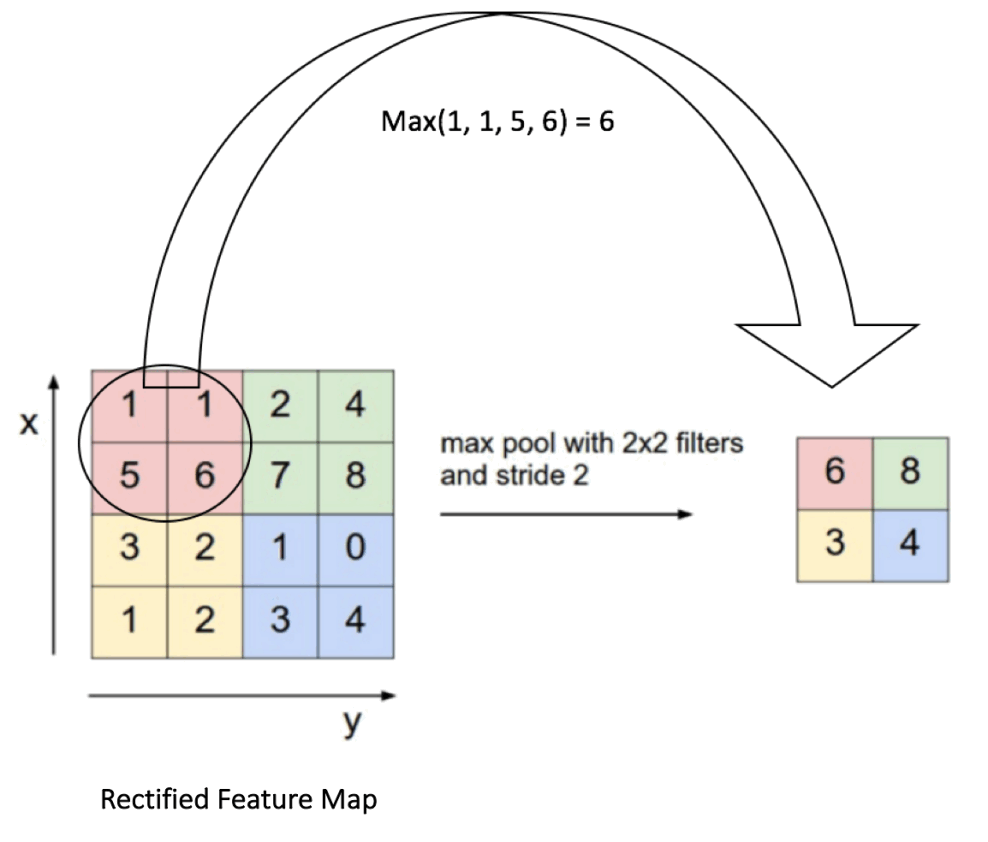
cnn_max_pooling.gif

Figure 7: Max Pooling operation on a Rectified Feature map (obtained after convolution + ReLU operation) by using a 2×2 window.

除了采样方式（最大值/平均值）外，子采用层还有两个重要配置参数：窗口大小（也称为 Kernel 大小）和 Stride（即步幅，在卷积层中也有 Stride 的概念，参见 1.1.2）。在图 7 的例子中，窗口大小为 2×2，步幅为 2。

子采样的作用还在于可以使得下一层的神经元对一些小的形态改变保持不变性，并拥有更大的感受野。

1.3. 典型卷积神经网络层组件

卷积神经网络层在不同文献中，可能出现不同的形式，一般有两组术语。如图 8 所示。

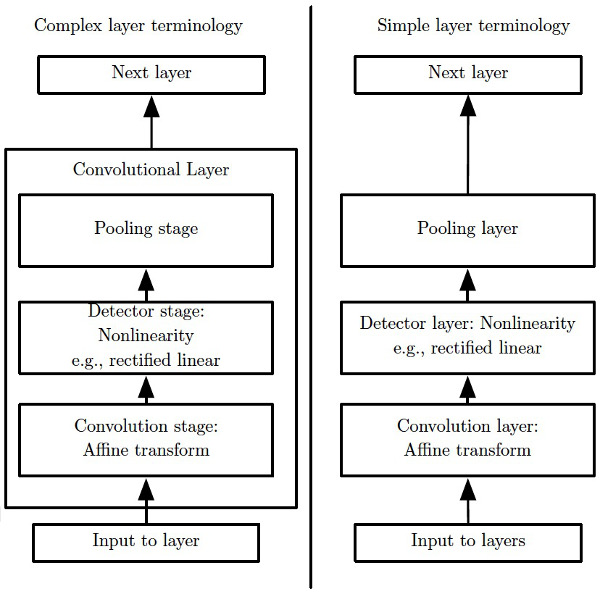
cnn_cnn_layer.jpg

Figure 8: 典型卷积神经网络层组件

2. 一些著名的 CNN 模型

2.1. LeNet-5

LeNet-5 由 LeCun 于 1998 年提出，它可以看作是 CNN 的正式开始。基于 LeNet-5 的手写数字识别系统在 90 年代被美国很多银行使用，用来识别支票上面的手写数字。

LeNet-5 模型如图 9 所示。

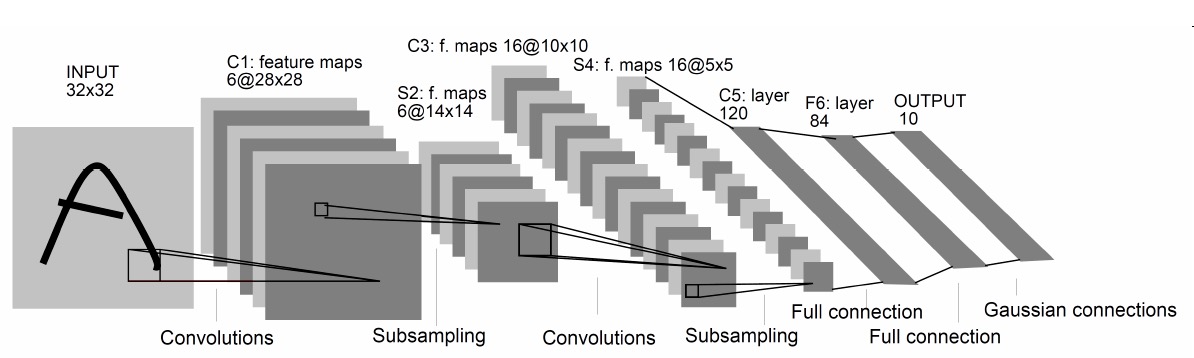
cnn_lenet5.jpg

Figure 9: LeNet-5 模型，图片来自 LeCun 原始论文

不计输入层，LeNet-5 共有 7 层，每一层的结构如下：
(1) 输入层：输入图像大小为 32×32 = 1024。
(2) C1 层：这一层是卷积层。滤波器的大小是 5×5=25，共有 6 个滤波器。得到 6 组大小为(32-5+1)×(32-5+1)=28×28=784 的 Feature Map。因此，C1 层的神经元个数为 6×784=4704。可训练参数个数为 6×25+6=156。连接数为 156×784=122304。（包括偏置在内，下同）。
(3) S2 层：这一层为子采样层。由 C1 层每组 Feature Map 中的 2×2 邻域点次采样为 1 个点，也就是 4 个数的平均。这一层的神经元个数为 14×14 = 196。可训练参数个数为 6×(1+1)=12。连接数为 6×196×(4+1)=122304（包括偏置的连接）。
(4) C3 层：这一层是卷积层，滤波器的大小也是 5×5，共有 16 个滤波器，得到 16 组大小为(14-5+1)×(14-5+1)=10×10 的 Feature Map。由于 S2 层输出是 6 组 Feature Map，这需要一个连接表来定义不同层 Feature Map 之间的依赖关系。LeNet-5 的连接表如图 10 所示。这样的连接机制的基本假设是：C3 层的最开始的 6 个 Feature Map 依赖于 S2 层的 Feature Map 的每 3 个连续子集。接下来的 6 个 Feature Map 依赖于 S2 层的 Feature Map 的每 4 个连续子集。再接下来的 3 个 Feature Map 依赖于 S2 层的 Feature Map 的每 4 个不连续子集。最后一个 Feature Map 依赖于 S2 层的所有 Feature Map。为什么采用上述的组合方式呢？论文中说有两个原因：1、减少参数；2、这种不对称的组合连接的方式有利于提取多种组合特征。

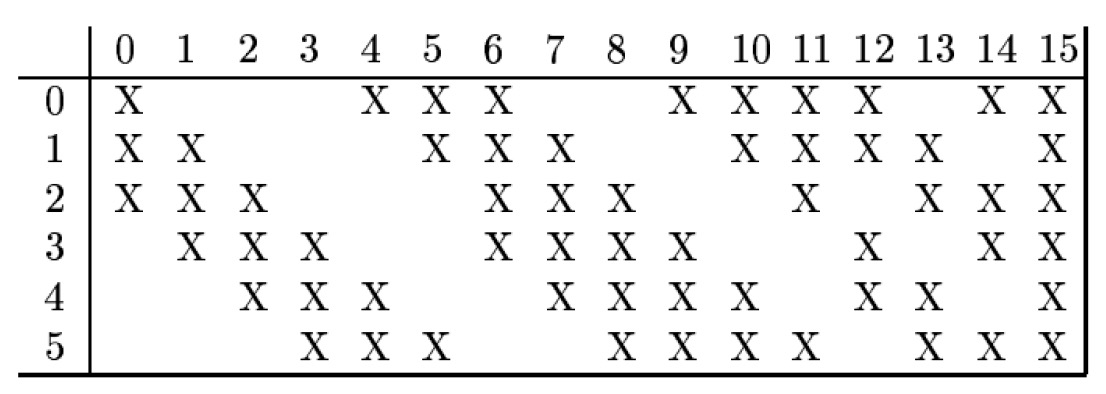
cnn_lenet5_c3.jpg

Figure 10: LeNet-5 中 C3 层的连接表，图片来自 LeCun 原始论文

图 10 的前两列表示：C3 层的第 0 个 Feature Map 仅由 S2 层的第 0、1、2 个 Feature Map 组合得到的（它仅使用了 S2 层的全部 6 组 Feature Map 中的 3 个，如图 11 所示）；C3 层的第 1 个 Feature Map 仅由 S2 层的第 1、2、3 个 Feature Map 组合得到的。

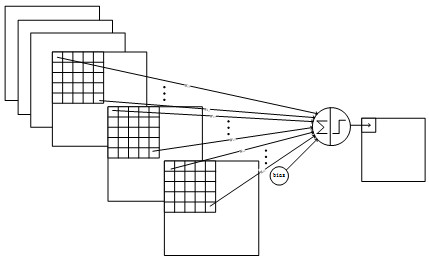
cnn_lenet5_c3_part.jpg

Figure 11: C3 层的第 0 个 Feature Map 仅由 S2 层的第 0、1、2 个 Feature Map 得到

(5) S4 层：这一层是一个子采样层，由 2×2 邻域点次采样为 1 个点，得到 16 组 5×5 大小的 Feature Map。
(6) C5 层：是一个卷积层。滤波器大小也为 5×5，由于第 4 层输出的 Feature Map 大小为 5×5，所以这一层输出的每个 Feature Map 有(5-5+1)×(5-5+1)=1×1 个神经元。C5 层的每个单元都与 S4 层的全部 16 个 Feature Map 相连（这种方式类似于图 10 中表格内容全部为 X），因此第五层相当于全连接层。C5 层共有 120 个滤波器。
(7) F6 层：F6 层是普通神经网络里面的隐藏层，在这里是为了将 120 维的 C5 降维成 84 维的 F6。F6 中的每一个神经元和 C5 层也形成了全连接，这是第二个全连接层。
(8) 输出层：由 10 个欧氏径向基函数（Radial Basis Function，RBF）函数组成。

2.2. AlexNet, VGG, GooLeNet, ResNet

表 1 是近年来提出的著名 CNN 模型。

Table 1: 一些著名的 CNN 模型
模型名 AlexNet VGG GoogLeNet ResNet
提出时间 2012 2014 2014 2015
层数 8 19 22 152
ImageNet Top-5 错误率 16.4% 7.3% 6.7% 3.57%

注 1：ImageNet 是目前世界上图像识别最大的数据库，由华裔人工智能专家李飞飞创建。
注 2：ImageNet 图像通常有多个可能类别，对每幅图像你可以同时预测 5 个类别标签，当其中有一次预测对了，结果都算对，如果 5 次全都错了，才算预测错误，这种分类错误率就是 Top-5 错误率。
注 3：人眼辨识的 ImageNet Top-5 错误率约为 5.1%，从表 1 中可知，机器（3.57%）已经超过了人类。

参考：
Stanford CS231n, Lecture 9: CNN Architectures: http://cs231n.stanford.edu/slides/2017/cs231n_2017_lecture9.pdf
CNN 的发展史：http://www.cnblogs.com/52machinelearning/p/5821591.html

3. 训练卷积神经网络

前面介绍的仅是 CNN 的结构特点。这里简单说明描述一下卷积神经网络的训练过程。

首先，回顾一下，利用“反向传播算法”训练全连接前馈神经网络的方法。其思路为：使用梯度下降法（如“批量梯度下降”或者“随机梯度下降法”）对模型各个参数进行迭代更新，我们需要不断计算的仅是在各个训练数据点处，损失函数对模型各个参数的偏导数，这个计算可通过 BP 算法的四个公式来进行：

\begin{align*} & \boldsymbol{\delta}^{(L)} = - (\boldsymbol{y} - \boldsymbol{a}^{(L)}) \odot f'(\boldsymbol{z}^{(L)}) \tag{BP-1} \\ & \boldsymbol{\delta}^{(l)} = \left((W^{(l+1)})^{\mathsf{T}} \boldsymbol{\delta}^{(l+1)} \right) \odot f'(\boldsymbol{z}^{(l)}) \tag{BP-2} \\ & \frac{\partial E}{\partial W^{(l)}} = \boldsymbol{\delta}^{(l)} (\boldsymbol{a}^{(l-1)})^{\mathsf{T}} \tag{BP-3} \\ & \frac{\partial E}{\partial b^{(l)}} = \boldsymbol{\delta}^l \tag{BP-4} \\ \end{align*}

关于上面公式的详细说明，请参考http://aandds.com/blog/neural-network-bp.html。

训练卷积神经网络和训练全连接前馈神经网络的思路也是一样的，都是梯度下降法。不同之处在于“反向传播”算法中梯度计算公式和全连接前馈神经网络的（即上面四个公式）有所区别。

在卷积神经网络中，每一个卷积层后都接着一个子采样层，然后不断重复。因此，我们需要分别计算卷积层和子采样层的梯度。

情况一，卷积层的梯度。我们假定卷积层为 \(l\) 层，子采样层为 \(l + 1\) 层。这时可以推导出由 \(\boldsymbol{\delta}^{(l+1)}\) 计算 \(\boldsymbol{\delta}^{(l)}\) ，再利用 \(\boldsymbol{\delta}^{(l)}\) 计算卷积层梯度的公式。
情况二，子采样层的梯度。我们假定子采样层为 \(l\) 层，卷积层为 \(l + 1\) 层。这时也可以推导出由 \(\boldsymbol{\delta}^{(l+1)}\) 计算 \(\boldsymbol{\delta}^{(l)}\) ，再利用 \(\boldsymbol{\delta}^{(l)}\) 计算子采样层梯度的公式。

这里不详细介绍如何推导CNN的梯度计算公式。可参考下面链接：
Notes on Convolutional Neural Networks, by Jake Bouvrie: http://cogprints.org/5869/1/cnn_tutorial.pdf
Deep Learning论文笔记之（四）CNN卷积神经网络推导和实现：http://blog.csdn.net/zouxy09/article/details/9993371

Author: cig01

Created: <2016-01-15 Fri>

Last updated: <2020-11-05 Thu>

Creator: Emacs 27.1 (Org mode 9.4)